题目内容
已知函数f(x)＝3x＋k(k为常数)，A(－2k，2)是函数y＝f－1(x)图象上的点．
(1)求实数k的值及函数y＝f－1(x)的解析式；
(2)将y＝f－1(x)的图象沿x轴向右平移3个单位，得函数 y＝g(x)的图象．求函数F(x)＝2f－1(x)－g(x)的最小值．
答案：
提示：
提示：
命题意图：本题主要考查函数与反函数的概念、函数图象的平移变换等． 解题思路：(1)∵A(－2k,2)是函数y＝f－1(x)图象上的点， ∴B(2，－2k)是函数y＝f(x)图象上的点． ∴－2k＝32＋k∴k＝－3．∴y＝f(x)＝3x－3(x>－3)． (2)∵y＝f－1(x)＝log3(x＋3)， ∴g(x)＝log3x(x>0)． ∴F(x)＝2y＝f－1(x)－g(x)＝log3 ∴当x＝3时，F(x)的最小值为1＋2log32． 评点：通过平移确定g(x)的表达式是解本题的关键，向右平移x→x－3，向左平移则x→x＋3．平移变换是基本的函数图象变换，也是高考的重点之一．
|
(
＋
l
练习册系列答案
阅读快车系列答案
相关题目
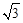sin ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
sin
ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
的最大值；
)>kg(x)对x∈[2,4]有解，求实数k的取值范围．
sin
ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
，无最小值