题目内容
（文）运货卡车以每小时x千米的速度匀速行驶1300千米，按交通法规限制40≤x≤100（单位：千米/小时）．假设汽油的价格是每升7元，而汽车每小时耗油(2+
)升，司机的工资是每小时30元．
（1）求这次行车总费用y关于x的表达式；
（2）当x为何值时，这次行车的总费用最低，并求出最低费用的值．（精确到0.01）
| x2 |
| 360 |
（1）求这次行车总费用y关于x的表达式；
（2）当x为何值时，这次行车的总费用最低，并求出最低费用的值．（精确到0.01）
（1）设行车所用时间为 t=
(h)，y=
×7×(2+
)+
，x∈[40，100]
所以，这次行车总费用y关于x的表达式是 y=
+
x(x∈[40，100])
（2）x∈[40，100]时，y，=-
+
＞0
所以 y=
+
x(x∈[40，100])为增函数．
所以，当x=40时，这次行车的总费用最低，最低费用为2441.11元
| 1300 |
| x |
| 1300 |
| x |
| x2 |
| 360 |
| 30×1300 |
| x |
所以，这次行车总费用y关于x的表达式是 y=
| 57200 |
| x |
| 455 |
| 18 |
（2）x∈[40，100]时，y，=-
| 57200 |
| x2 |
| 455 |
| 18 |
所以 y=
| 57200 |
| x |
| 455 |
| 18 |
所以，当x=40时，这次行车的总费用最低，最低费用为2441.11元
练习册系列答案
巧学巧练系列答案
相关题目
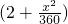升，司机的工资是每小时30元．