题目内容
已知数列{an}的前n项和Sn=﹣an﹣( )n﹣1+2(n为正整数).
)n﹣1+2(n为正整数).
(1)令bn=2nan,求证数列{bn}是等差数列,并求数列{an}的通项公式;
(2)令cn=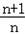 an,若Tn=c1+c2+…+cn,求Tn.
an,若Tn=c1+c2+…+cn,求Tn.
 )n﹣1+2(n为正整数).
)n﹣1+2(n为正整数).(1)令bn=2nan,求证数列{bn}是等差数列,并求数列{an}的通项公式;
(2)令cn=
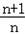 an,若Tn=c1+c2+…+cn,求Tn.
an,若Tn=c1+c2+…+cn,求Tn.解:(1)在Sn=﹣an﹣( )n﹣1+2中
)n﹣1+2中
令n=1可得
S1=﹣a1﹣1+2=a1
即a1=
当n≥2时,an=Sn﹣S n﹣1=﹣an+a n﹣1+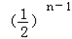
∴2an=a n﹣1+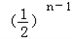
即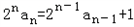
∵bn=2nan,
∴bn﹣b n﹣1=1
即当n≥2时,bn﹣b n﹣1=1
又∵b1=2a1=1
∴数列{bn}是首项和公差均为1的等差数列.
∴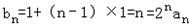
∴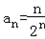
(2)由(1)得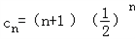 ,
,
∴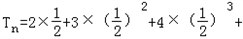 …+(n+1)
…+(n+1)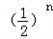 ①
①
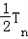 =2×
=2×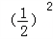 +3×
+3×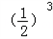 +4×
+4×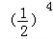 +…+(n+1)
+…+(n+1)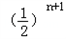 ②
②
由①﹣②得
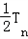 =1+
=1+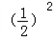 +
+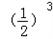 +…+
+…+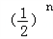 ﹣(n+1)
﹣(n+1)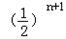 =
= ﹣
﹣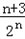
∴Tn=3﹣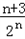
 )n﹣1+2中
)n﹣1+2中令n=1可得
S1=﹣a1﹣1+2=a1
即a1=

当n≥2时,an=Sn﹣S n﹣1=﹣an+a n﹣1+
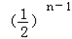
∴2an=a n﹣1+
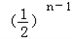
即
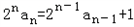
∵bn=2nan,
∴bn﹣b n﹣1=1
即当n≥2时,bn﹣b n﹣1=1
又∵b1=2a1=1
∴数列{bn}是首项和公差均为1的等差数列.
∴
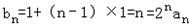
∴
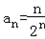
(2)由(1)得
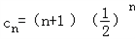 ,
,∴
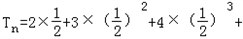 …+(n+1)
…+(n+1)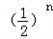 ①
①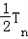 =2×
=2×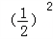 +3×
+3×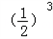 +4×
+4×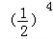 +…+(n+1)
+…+(n+1)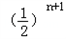 ②
②由①﹣②得
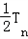 =1+
=1+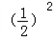 +
+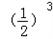 +…+
+…+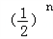 ﹣(n+1)
﹣(n+1)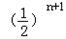 =
= ﹣
﹣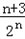
∴Tn=3﹣
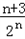

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |