题目内容
已知函数f(x)=2x2-10x,(x∈R),问是否存在自然数m,使得方程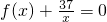 在区间(m,m+1)内有且仅有两个不等的实数解?若存在,求出m的值;若不存在,请说明理由.
在区间(m,m+1)内有且仅有两个不等的实数解?若存在,求出m的值;若不存在,请说明理由.
解:依题意,问题等价于方程2x3-10x2+37=0在(m,m+1)内有且仅有两个不等的实数根,
令h(x)=2x3-10x2+37,
h′(x)=6x2-20x=6x(x- ),
),
当x∈(0, )时,h′(x)<0,h(x)在区间(0,
)时,h′(x)<0,h(x)在区间(0, )上单调递减;
)上单调递减;
当x∈( ,+∞)时,h′(x)>0,h(x)在区间(
,+∞)时,h′(x)>0,h(x)在区间( ,+∞)上单调递增;…4分
,+∞)上单调递增;…4分
由于h(3)=1>0,h( )=-
)=- <0,h(4)=5>0,…7分
<0,h(4)=5>0,…7分
所以方程h(x)=0在(3, ),(
),( ,4)内分别有唯一实数根,而在(0,3),(4,+∞)内没有实数根…10分
,4)内分别有唯一实数根,而在(0,3),(4,+∞)内没有实数根…10分
所以存在唯一自然数m=3使得方程f(x)+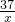 =0在区间(m,m+1)内有且仅有两个不等的实数解.…12分
=0在区间(m,m+1)内有且仅有两个不等的实数解.…12分
分析:依题意,将f(x)+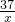 =0在区间(m,m+1)内有且仅有两个不等的实数解转化为2x3-10x2+37=0在(m,m+1)内有且仅有两个不等的实数根,通过导数可分析得方程h(x)=0在(3,
=0在区间(m,m+1)内有且仅有两个不等的实数解转化为2x3-10x2+37=0在(m,m+1)内有且仅有两个不等的实数根,通过导数可分析得方程h(x)=0在(3, ),(
),( ,4)内分别有唯一实数根,而在(0,3),(4,+∞)内没有实数根,从而可得答案.
,4)内分别有唯一实数根,而在(0,3),(4,+∞)内没有实数根,从而可得答案.
点评:本题考查利用导数研究函数的单调性,考查根的存在性及根的个数判断,考查等价转化思想与分类讨论思想的综合运用,属于难题.
令h(x)=2x3-10x2+37,
h′(x)=6x2-20x=6x(x-
 ),
),当x∈(0,
 )时,h′(x)<0,h(x)在区间(0,
)时,h′(x)<0,h(x)在区间(0, )上单调递减;
)上单调递减;当x∈(
 ,+∞)时,h′(x)>0,h(x)在区间(
,+∞)时,h′(x)>0,h(x)在区间( ,+∞)上单调递增;…4分
,+∞)上单调递增;…4分由于h(3)=1>0,h(
 )=-
)=- <0,h(4)=5>0,…7分
<0,h(4)=5>0,…7分所以方程h(x)=0在(3,
 ),(
),( ,4)内分别有唯一实数根,而在(0,3),(4,+∞)内没有实数根…10分
,4)内分别有唯一实数根,而在(0,3),(4,+∞)内没有实数根…10分所以存在唯一自然数m=3使得方程f(x)+
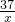 =0在区间(m,m+1)内有且仅有两个不等的实数解.…12分
=0在区间(m,m+1)内有且仅有两个不等的实数解.…12分分析:依题意,将f(x)+
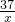 =0在区间(m,m+1)内有且仅有两个不等的实数解转化为2x3-10x2+37=0在(m,m+1)内有且仅有两个不等的实数根,通过导数可分析得方程h(x)=0在(3,
=0在区间(m,m+1)内有且仅有两个不等的实数解转化为2x3-10x2+37=0在(m,m+1)内有且仅有两个不等的实数根,通过导数可分析得方程h(x)=0在(3, ),(
),( ,4)内分别有唯一实数根,而在(0,3),(4,+∞)内没有实数根,从而可得答案.
,4)内分别有唯一实数根,而在(0,3),(4,+∞)内没有实数根,从而可得答案.点评:本题考查利用导数研究函数的单调性,考查根的存在性及根的个数判断,考查等价转化思想与分类讨论思想的综合运用,属于难题.

练习册系列答案
相关题目