题目内容
已知位于半径为R的地球上两点A、B分别位于A（南纬45°，东经31°），B（南纬45°，西经59°），则A、B两点的最短距离为
R
R．
| π |
| 3 |
| π |
| 3 |
分析：先在南纬45°的小圆上，计算AB长，进而在△AOB中，求∠AOB，从而利用弧长公式可求A、B两点的最短距离
解答：解：设南纬45°的圆心为C，O为球心，则
∵A、B分别位于A（南纬45°，东经31°），B（南纬45°，西经59°），
∴CA=CB=
R，∠ACB=90°
∴AB=R
在△AOB中，OA=OB=AB=R
∴∠AOB=
∴A、B两点的最短距离为
R
故答案为：
R
∵A、B分别位于A（南纬45°，东经31°），B（南纬45°，西经59°），
∴CA=CB=
| ||
| 2 |
∴AB=R
在△AOB中，OA=OB=AB=R
∴∠AOB=
| π |
| 3 |
∴A、B两点的最短距离为
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题以球为载体，考查球面距离，考查球面上两点的最短距离，属于基础题．
练习册系列答案
相关题目
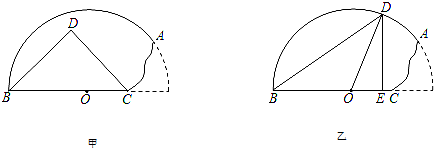
，残缺部分位于过点C的竖直线的右侧．现要在这块材料上截出一个直角三角形，有两种设计方案：如图甲，以BC为斜边；如图乙，直角顶点E在线段OC上，且另一个顶点D在
上．要使截出的直角三角形的面积最大，应该选择哪一种方案？请说明理由，并求出截得直角三角形面积的最大值．