题目内容
如图，已知正方体ABCD—A1B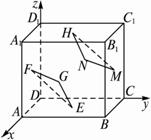
证明：如图，建立空间直角坐标系D—xyz,设正方体的棱长为2，易得E（1，1，0），F（1，0，1），G（2，1，1），H（1，1，2），M（1，2，1），N（0，1，1）.?
∴
=(0,-1,1),
=(1,0,1),?
=(0,1,-1),
=(-1,0,-1).?
设m=(x1,y1,z1),n=(x2,y2,z2)分别是平面EFG、平面HMN的法向量，?
由
令x1=1，得m=(1,-1,-1).?
由
令x2=1,得n=(1,-1,-1).?
∴m=n,故m∥n，,即平面EFG∥平面HMN.
练习册系列答案
相关题目
8、如图，已知正方体ABCD-A1B1C1D1的棱长为3，点E，F在线段AB上，点M在线段B1C1上，点N在线段C1D1上，且EF=1，D1N=x，AE=y，M是B1C1的中点，则四面体MNEF的体积（ ）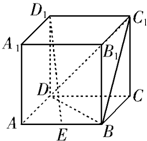
如图，已知正方体ABCD-A1B1C1D1的棱长为2，点E为棱AB的中点．
如图，已知正方体ABCD-A1B1C1D1的棱长为2，E、F分别是D1C、AB的中点．
如图，已知正方体ABCD-A1B1C1D1的棱长为2，点P，Q，R分别是棱AB，CC1，D1A1的中点．
（2012•宝山区一模）如图，已知正方体ABCD-A1B1C1D1 的棱长为2，E，F分别是BB1，CD的中点．