题目内容
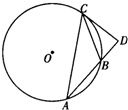
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是: .B.(几何证明选做题)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若
 ,
, ,则
,则 的值为 .
的值为 .C.(坐标系与参数方程选做题)设曲线C的参数方程为
 (θ为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
(θ为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为 ,则曲线C上到直线l距离为
,则曲线C上到直线l距离为 的点的个数为: .
的点的个数为: .
【答案】分析:A、根据绝对值的几何意义,我们易分析出|x+3|-|x+2|表示数轴上的x到-2和-3的距离之和,求出|x+3|-|x+2|的最小值后,即可得到实数a的取值范围.
B、利用割线定理我们易求出PA、PB、PC、PD的比例,由圆外接四边形定理,我们易判断出△PBC∽△PDA,根据相似三角形对应边成比例,我们易得到答案.
C、根据已知中曲线和直线的极坐标方程,我们易求出圆的标准方程和直线的一般方程,判断出直线与圆的位置关系,即可得到结论.
解答:解:A∵关于x的不等式|x+3|-|x+2|≥log2a有解,
|x+3|-|x+2|表示数轴上的x到-3和-2的距离之差,其最小值等于-1,最大值是1,
由题意log2a≤1,
∴0<a≤2.
故答案为:(0,2]
B、∵ ,
, ,
,
∴设 PB=m,PC=n,则 PA=2 m,PD=3n,
由切割线定理得:PA•PB=PC•PD
即2m2=3n2
故m:n= :
:
由圆外接四边形定理得:∠PBC=∠PDA,∠PCB=∠PAD
∴△PBC∽△PDA
∴ =
= =
= =
=
故答案为:
C、∵曲线C的参数方程为 (θ为参数),
(θ为参数),
∴曲线C的标准方程这:(x-3)2+(y+1)2=8,它表示以(3,-1)点为圆心,以2 为半径的圆
为半径的圆
又∵直线l的极坐标方程为 ,
,
∴它的一般方程为x-y-2=0
∵(3,-1)点到直线x-y-2=0的距离为 ,等于圆半径的一半
,等于圆半径的一半
故曲线C上到直线l距离为 的点的个数为3个
的点的个数为3个
故答案为:3
点评:本题考查的知识点是简单曲线的极坐标方程,与圆有关的比例线段,绝对不等式的解法,A中关键是掌握绝对值的几何意义,B中关系是求出PA、PB、PC、PD的比例,C中的关键是求出圆的标准方程和直线的一般方程.
B、利用割线定理我们易求出PA、PB、PC、PD的比例,由圆外接四边形定理,我们易判断出△PBC∽△PDA,根据相似三角形对应边成比例,我们易得到答案.
C、根据已知中曲线和直线的极坐标方程,我们易求出圆的标准方程和直线的一般方程,判断出直线与圆的位置关系,即可得到结论.
解答:解:A∵关于x的不等式|x+3|-|x+2|≥log2a有解,
|x+3|-|x+2|表示数轴上的x到-3和-2的距离之差,其最小值等于-1,最大值是1,
由题意log2a≤1,
∴0<a≤2.
故答案为:(0,2]
B、∵
 ,
, ,
,∴设 PB=m,PC=n,则 PA=2 m,PD=3n,
由切割线定理得:PA•PB=PC•PD
即2m2=3n2
故m:n=
 :
:
由圆外接四边形定理得:∠PBC=∠PDA,∠PCB=∠PAD
∴△PBC∽△PDA
∴
 =
= =
= =
=
故答案为:

C、∵曲线C的参数方程为
 (θ为参数),
(θ为参数),∴曲线C的标准方程这:(x-3)2+(y+1)2=8,它表示以(3,-1)点为圆心,以2
 为半径的圆
为半径的圆又∵直线l的极坐标方程为
 ,
,∴它的一般方程为x-y-2=0
∵(3,-1)点到直线x-y-2=0的距离为
 ,等于圆半径的一半
,等于圆半径的一半故曲线C上到直线l距离为
 的点的个数为3个
的点的个数为3个故答案为:3
点评:本题考查的知识点是简单曲线的极坐标方程,与圆有关的比例线段,绝对不等式的解法,A中关键是掌握绝对值的几何意义,B中关系是求出PA、PB、PC、PD的比例,C中的关键是求出圆的标准方程和直线的一般方程.

练习册系列答案
相关题目
 A.(不等式选做题)
A.(不等式选做题)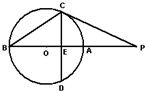 A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) 选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)
选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)