题目内容
已知正三棱柱ABC-A1B1C1的底面边长为2,高为1,过顶点A作一平面α与侧面BCC1B1交于EF,且EF∥BC.若平面α与底面ABC所成二面角的大小为x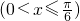 ,四边形BCEF面积为y,则函数y=f(x)的图象大致是
,四边形BCEF面积为y,则函数y=f(x)的图象大致是
- A.
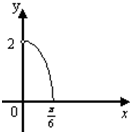
- B.
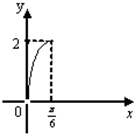
- C.
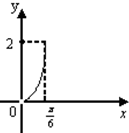
- D.
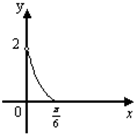
C
分析:先作出平面α与底面ABC所成二面角的平面角x,如图为∠GAH,在直角三角形AGH中用x,及AH= 表示出GH,再利用四边形BCEF面积为y=BC×GH求出f(x),根据解析式作简图,与选项对应.
表示出GH,再利用四边形BCEF面积为y=BC×GH求出f(x),根据解析式作简图,与选项对应.
解答:如图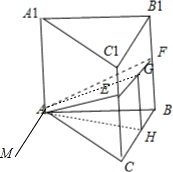 过A作AM∥BC,H,G是BC,EF中点,则 AH⊥BC,∴AH⊥AM,在等腰三角形△AEF中,AG⊥EF,∵EF∥BC.∴AG⊥AM,∴∠GAH是平面α与底面ABC所成二面角的平面角.∴∠GAH=x,tanx=
过A作AM∥BC,H,G是BC,EF中点,则 AH⊥BC,∴AH⊥AM,在等腰三角形△AEF中,AG⊥EF,∵EF∥BC.∴AG⊥AM,∴∠GAH是平面α与底面ABC所成二面角的平面角.∴∠GAH=x,tanx=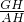 ,∴GH=
,∴GH= tanx
tanx
∴四边形BCEF面积为y=f(x)=BC×GH=2 tanx,根据正切函数图象可知C符合.
tanx,根据正切函数图象可知C符合.
故选C
点评:本题考查二面角的概念,函数的图象,是函数与空间几何体的结合.是好题.
分析:先作出平面α与底面ABC所成二面角的平面角x,如图为∠GAH,在直角三角形AGH中用x,及AH=
 表示出GH,再利用四边形BCEF面积为y=BC×GH求出f(x),根据解析式作简图,与选项对应.
表示出GH,再利用四边形BCEF面积为y=BC×GH求出f(x),根据解析式作简图,与选项对应.解答:如图
 过A作AM∥BC,H,G是BC,EF中点,则 AH⊥BC,∴AH⊥AM,在等腰三角形△AEF中,AG⊥EF,∵EF∥BC.∴AG⊥AM,∴∠GAH是平面α与底面ABC所成二面角的平面角.∴∠GAH=x,tanx=
过A作AM∥BC,H,G是BC,EF中点,则 AH⊥BC,∴AH⊥AM,在等腰三角形△AEF中,AG⊥EF,∵EF∥BC.∴AG⊥AM,∴∠GAH是平面α与底面ABC所成二面角的平面角.∴∠GAH=x,tanx=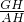 ,∴GH=
,∴GH= tanx
tanx∴四边形BCEF面积为y=f(x)=BC×GH=2
 tanx,根据正切函数图象可知C符合.
tanx,根据正切函数图象可知C符合.故选C
点评:本题考查二面角的概念,函数的图象,是函数与空间几何体的结合.是好题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
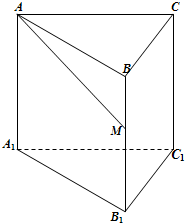 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ. 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.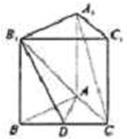 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.