题目内容
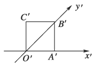
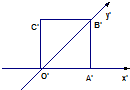 如图,正方形O′A′B′C′的边长为a,它是水平放置的一个平面图形的直观图,则原图形的面积是
如图,正方形O′A′B′C′的边长为a,它是水平放置的一个平面图形的直观图,则原图形的面积是2
a2
| 2 |
2
a2
.| 2 |
分析:根据题意将正方形O′A′B′C′还原到直角坐标系中,得到平行四边形OABC,其中OA=a,对角线OB=2
a且OB⊥OC,利用平行四边形的面积公式即可算出其面积.
| 2 |
解答:解: 根据题意,得
根据题意,得
将正方形O′A′B′C′还原到直角坐标系中的四边形OABC
可得OA=O'A'=a,OB=2O'B'=2
a,且BC
OA
∴平行四边形OABC的面积为S=OA•0B=a•2
a=2
a2
即直观图的原图形的面积为2
a2
故答案为:2
a2
 根据题意,得
根据题意,得将正方形O′A′B′C′还原到直角坐标系中的四边形OABC
可得OA=O'A'=a,OB=2O'B'=2
| 2 |
| ∥ |
. |
∴平行四边形OABC的面积为S=OA•0B=a•2
| 2 |
| 2 |
即直观图的原图形的面积为2
| 2 |
故答案为:2
| 2 |
点评:本题给出四边形的直观图形状,求原图形的面积.着重考查了平行四边形的面积公式和平面图形直观图的理解等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方形O'A'B'C'的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积是
如图,正方形O'A'B'C'的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积是 如图,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图的周长是( )
如图,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图的周长是( )