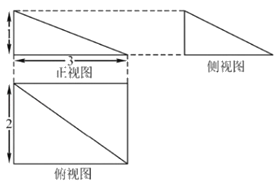
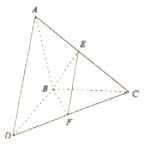
题目内容
【题目】正三棱锥![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,过
,过![]() 的平面截三棱锥
的平面截三棱锥![]() 的外接球所得截面的面积范围为________.
的外接球所得截面的面积范围为________.
【答案】![]()
【解析】
根据题意可将正三棱锥![]() 放到以
放到以![]() 为棱长的正方体中,再根据正三棱锥
为棱长的正方体中,再根据正三棱锥![]() 的外接球与该正方体的外接球相同,再根据球心到
的外接球与该正方体的外接球相同,再根据球心到![]() 的距离分析截面的范围即可.
的距离分析截面的范围即可.
因为正三棱锥![]() 中
中![]() ,
,![]() ,故
,故![]() ,
,![]() .因为
.因为![]() ,故
,故![]() .同理
.同理![]() ,
,![]() .
.
因此可正三棱锥![]() 是棱长为
是棱长为![]() 正方体的一角.
正方体的一角.
此时正三棱锥![]() 的外接球
的外接球![]() 与正方体外接球相同.
与正方体外接球相同.
且球![]() 的半径
的半径![]() .
.
又球的最大截面圆为过球心的圆,所以过![]() 的平面截三棱锥
的平面截三棱锥![]() 的外接球所得截面的面积最大值为
的外接球所得截面的面积最大值为![]() .
.
又![]() 为
为![]() 中点,根据正方体的结构特征可知
中点,根据正方体的结构特征可知![]() .当
.当![]() 垂直于过
垂直于过![]() 的截面时,截面圆半径的最小值
的截面时,截面圆半径的最小值![]() .所以过
.所以过![]() 的平面截三棱锥
的平面截三棱锥![]() 的外接球所得截面的面积最大值为
的外接球所得截面的面积最大值为![]() .
.
因此![]() 的平面截三棱锥
的平面截三棱锥![]() 的外接球所得截面的面积范围为
的外接球所得截面的面积范围为![]() .
.

故答案为:![]()

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
【题目】在新高考改革中,打破了文理分科的“![]() ”模式,不少省份采用了“
”模式,不少省份采用了“![]() ”,“
”,“![]() ”,“
”,“![]() ”等模式.其中“
”等模式.其中“![]() ”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含男生110人,求n的值及抽取到的女生人数;
(2)在(1)的情况下对抽取到的n名同学“选物理”和“选历史”进行问卷调查,得到下列2×2列联表.请将列联表补充完整,并判断是否有99%的把握认为选科目与性别有关?
选物理 | 选历史 | 合计 | |
男生 | 90 | ||
女生 | 30 | ||
合计 |
(3)在(2)的条件下,从抽取的“选历史”的学生中按性别分层抽样再抽取5名,再从这5名学生中抽取2人了解选政治、地理、化学、生物的情况,求2人至少有1名男生的概率.
参考公式: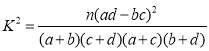 .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |