题目内容
已知数列{an}满足:a1=1,nan+1=2(n十1)an+n(n+1),(n∈N*),(I)若
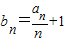 ,试证明数列{bn}为等比数列;
,试证明数列{bn}为等比数列;(II)求数列{an}的通项公式an与前n项和Sn.
【答案】分析:(Ⅰ)利用数列递推式,证明bn+1=2bn,即可证明数列{bn}为等比数列;
(II)利用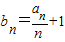 ,可数列{an}的通项公式an,利用错位相减法可求数列的和.
,可数列{an}的通项公式an,利用错位相减法可求数列的和.
解答:(Ⅰ)证明:∵nan+1=2(n+1)an+n(n+1),∴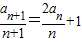 ,…(2分)
,…(2分)
∴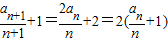 ,即bn+1=2bn,
,即bn+1=2bn,
又b1=2,所以{bn}是以2为首项,2为公比的等比数列.…(6分)
(Ⅱ)解:由(Ⅰ)知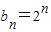 ,∴
,∴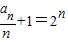 ,∴
,∴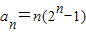 ,…(8分)
,…(8分)
∴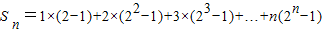 =1×2+2×22+3×23+…+n•2n-(1+2+3+…+n)=
=1×2+2×22+3×23+…+n•2n-(1+2+3+…+n)=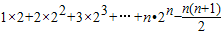 .…(10分)
.…(10分)
令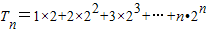 ,
,
则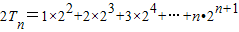 ,
,
两式相减得: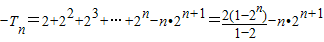 ,
,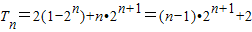 .…(12分)
.…(12分)
∴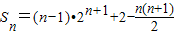 .…(13分)
.…(13分)
点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项与求和,正确运用求和方法是关键.
(II)利用
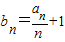 ,可数列{an}的通项公式an,利用错位相减法可求数列的和.
,可数列{an}的通项公式an,利用错位相减法可求数列的和.解答:(Ⅰ)证明:∵nan+1=2(n+1)an+n(n+1),∴
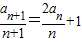 ,…(2分)
,…(2分)∴
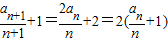 ,即bn+1=2bn,
,即bn+1=2bn,又b1=2,所以{bn}是以2为首项,2为公比的等比数列.…(6分)
(Ⅱ)解:由(Ⅰ)知
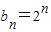 ,∴
,∴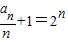 ,∴
,∴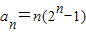 ,…(8分)
,…(8分)∴
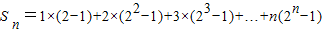 =1×2+2×22+3×23+…+n•2n-(1+2+3+…+n)=
=1×2+2×22+3×23+…+n•2n-(1+2+3+…+n)=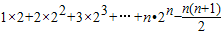 .…(10分)
.…(10分)令
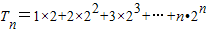 ,
,则
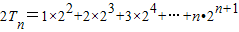 ,
,两式相减得:
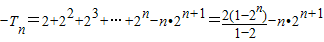 ,
,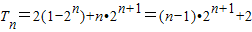 .…(12分)
.…(12分)∴
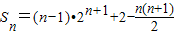 .…(13分)
.…(13分)点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项与求和,正确运用求和方法是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目