Question

已知x、y满足不等式组求使z=160x+252y取得最小值的非负整数点.

   

Answer 1

思路分析:先找出可行域中的所有整点,再寻求其中符合题意的整点.

    解:不等式组表示的平面区域如图所示.

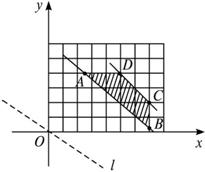
    其可行域为四边形ABCD及其内部,

    它的顶点坐标是A(,4),B(7,),C(7,2),D(5,4).

    结合图形可知,在四边形区域内,横坐标与纵坐标都是非负整数的点有

(3,4),(4,3),(4,4),(5,2),(5,3),(5,4),(6,2),(6,3),(7,1),(7,2).

    作直线l:160x+252y=0,将l向右上方平行移动,

    可发现它与上述点中最先接触到的整点是(5,2),

    所以在点(5,2)处得到的z的值最小,

    此时z_min=160×5+252×2=1 304.

    思维启示:对于线性规划中的最优整数解问题,当解方程组得到的解不是整数解时,常用下面的一些方法求解.

(1)平移直线法:先在可行域中画网格,再描整点,平移直线l,最先经过或最后经过的整点坐标就是最优解.

(2)检验优值法:当可行域中整点个数较少时,可将整点坐标逐一代入目标函数求值,经过比较得出最优解.

(3)调整优值法:先求非整点最优解,再借助于不定方程知识调整最优解.