题目内容
如图，在四棱锥V—ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD.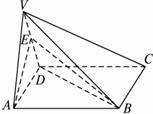
(1)证明AB⊥平面VAD；
(2)求面VAD与面VDB所成的二面角的大小.
解法一：(1)证明：平面VAD⊥平面ABCD
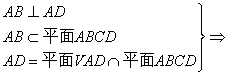AB⊥平面VAD.?
(2)取VD的中点E，连结AE、BE.?
∵△VAD是正三角形，∴AE⊥VD,AE=
AD.?
∵AB⊥平面VAD，∴AB⊥AE.?
又由三垂线定理知BE⊥VD，因此tan∠AEB=
,即得所求二面角的大小为arctan
.?
解法二：以D为坐标原点，建立如图所示的坐标图系.?
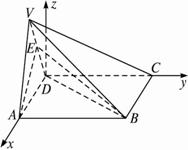
(1)证明：不妨设A(1,0，0)，则?B(1,1，0)?，V(
,0,
),
=(0,1,0),
=(
,0,- 
).?
由
•
=0,得AB⊥VA.?
又AB⊥AD，因而AB与平面VAD内两条相交直线VA、AD都垂直，∴AB⊥平面VAD.?
(2)设E为DV中点，则E(
,0,
),
=(
,0,-
),
=(
,1,-
),
=(
,0,
).?
由
•
=0,得EB⊥DV.?
又EA⊥DV，因此∠AEB是所求二面角的平面角.?
cos〈
,
〉=
,?
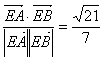解得所求二面角的大小为arccos
.
练习册系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
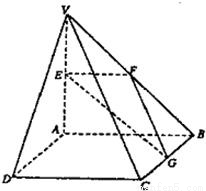
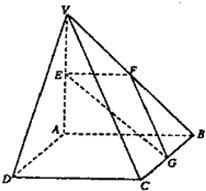如图，在四棱锥V-ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点．
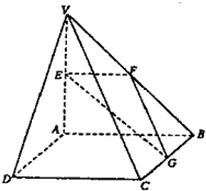如图，在四棱锥V-ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点．
