题目内容
命题p:△ABC及点G满足 ;命题q:G是△ABC的重心,则p是q的
;命题q:G是△ABC的重心,则p是q的
- A.充分不必要条件
- B.必要非充分条件
- C.充要条件
- D.既不充分又不必要
C
分析:先判断充分性,由命题p成立,结合向量的运算法则和几何意义,推出 ,得G为△ABC的重心;
,得G为△ABC的重心;
推出命题q成立,故充分性成立.
再判断必要性,设G是△ABC的重心,由重心的性质得 ,得出命题p中的等式成立,命题p成立,故必要性成立.
,得出命题p中的等式成立,命题p成立,故必要性成立.
解答: 如图:充分性:取BC的中点D,连接GD,并延长至E,使|DE|=|GD|,则四边形BECG为平行四边形,
如图:充分性:取BC的中点D,连接GD,并延长至E,使|DE|=|GD|,则四边形BECG为平行四边形,
∴ .又
.又 ,
,
∴ ,即G、A、D三点共线,且G为三等分点,故G为△ABC的重心;
,即G、A、D三点共线,且G为三等分点,故G为△ABC的重心;
必要性:设G是△ABC的重心,则G是△ABC的三边中线的交点,∴ ,
,
又-2 =-(
=-(  +
+ ),∴
),∴ .∴命题p成立,故必要性成立.
.∴命题p成立,故必要性成立.
综上,则p是q的充要条件.
点评:本题考查向量运算的法则和几何意义,三角形重心的性质,充分条件、必要条件的判断.
分析:先判断充分性,由命题p成立,结合向量的运算法则和几何意义,推出
 ,得G为△ABC的重心;
,得G为△ABC的重心; 推出命题q成立,故充分性成立.
再判断必要性,设G是△ABC的重心,由重心的性质得
 ,得出命题p中的等式成立,命题p成立,故必要性成立.
,得出命题p中的等式成立,命题p成立,故必要性成立.解答:
 如图:充分性:取BC的中点D,连接GD,并延长至E,使|DE|=|GD|,则四边形BECG为平行四边形,
如图:充分性:取BC的中点D,连接GD,并延长至E,使|DE|=|GD|,则四边形BECG为平行四边形,∴
 .又
.又 ,
,∴
 ,即G、A、D三点共线,且G为三等分点,故G为△ABC的重心;
,即G、A、D三点共线,且G为三等分点,故G为△ABC的重心;必要性:设G是△ABC的重心,则G是△ABC的三边中线的交点,∴
 ,
,又-2
 =-(
=-(  +
+ ),∴
),∴ .∴命题p成立,故必要性成立.
.∴命题p成立,故必要性成立.综上,则p是q的充要条件.
点评:本题考查向量运算的法则和几何意义,三角形重心的性质,充分条件、必要条件的判断.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
命题p:△ABC及点G满足
+
+
=0;命题q:G是△ABC的重心,则p是q的( )
| GA |
| GB |
| GC |
| A、充分不必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分又不必要 |
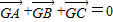 ;命题q:G是△ABC的重心,则p是q的( )
;命题q:G是△ABC的重心,则p是q的( )