Question

已知命题P：存在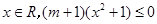， 命题Q：任意 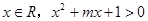恒成立。若P且Q为假命题，求实数m的取值范围？

Answer 1

m<=-2或m>=2

解析试题分析：p且q为假命题，说明p假或q假，
而p：存在m属于R，m+1<0一定是真命题，所以只能是q为假。
即存在x使得x^2+mx+1>0不成立，所以m^2-4>=0，解得m范围是m<=-2或m>=2
考点：复合命题
点评：主要是考查了复合命题的真值，以及全称命题和特称命题的理解运用，属于中档题。