题目内容
已知函数f(x)=sin cos
cos +
+ cos2
cos2 .
.
(1)将f(x)写成Asin(ωx+φ)+h(A>0)的形式,并求其图象对称中心的横坐标;
(2)若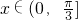 求函数的值域.
求函数的值域.
解:(1)∵sin cos
cos =
= sin
sin ,cos2
,cos2 =
= (1+cos
(1+cos )
)
∴f(x)=sin cos
cos +
+ cos2
cos2
= sin
sin +
+ (1+cos
(1+cos )=sin(
)=sin( +
+ )+
)+
令 +
+ =kπ(k∈Z),解之得x=-
=kπ(k∈Z),解之得x=- +
+ kπ(k∈Z)
kπ(k∈Z)
∴函数f(x)图象的对称中心横坐标为- +
+ kπ(k∈Z).
kπ(k∈Z).
(2)∵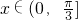 ,∴
,∴ +
+ ∈(
∈( ,
, ]
]
因此, <sin(
<sin( +
+ )≤1,可得
)≤1,可得 sin(
sin( +
+ )+
)+ ≤1+
≤1+
即函数当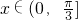 时的值域为(
时的值域为( ,1+
,1+ ].
].
分析:(1)利用二倍角的三角函数公式,结合辅助角公式化简整理得:f(x)=sin( +
+ )+
)+ .再
.再 +
+ =kπ(k∈Z),解出x=-
=kπ(k∈Z),解出x=- +
+ kπ,即得函数f(x)图象的对称中心横坐标.
kπ,即得函数f(x)图象的对称中心横坐标.
(2)当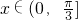 时,可得
时,可得 +
+ ∈(
∈( ,
, ],由此结合正弦函数的图象与性质,即可得到函数当
],由此结合正弦函数的图象与性质,即可得到函数当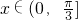 时的值域.
时的值域.
点评:本题给出三角函数表达式,求函数图象的对称中心并求闭区间上的值域,着重考查了二倍角的三角函数公式、辅助角公式和正弦函数的图象与性质等知识,属于中档题.
 cos
cos =
= sin
sin ,cos2
,cos2 =
= (1+cos
(1+cos )
)∴f(x)=sin
 cos
cos +
+ cos2
cos2
=
 sin
sin +
+ (1+cos
(1+cos )=sin(
)=sin( +
+ )+
)+
令
 +
+ =kπ(k∈Z),解之得x=-
=kπ(k∈Z),解之得x=- +
+ kπ(k∈Z)
kπ(k∈Z)∴函数f(x)图象的对称中心横坐标为-
 +
+ kπ(k∈Z).
kπ(k∈Z).(2)∵
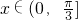 ,∴
,∴ +
+ ∈(
∈( ,
, ]
]因此,
 <sin(
<sin( +
+ )≤1,可得
)≤1,可得 sin(
sin( +
+ )+
)+ ≤1+
≤1+
即函数当
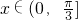 时的值域为(
时的值域为( ,1+
,1+ ].
].分析:(1)利用二倍角的三角函数公式,结合辅助角公式化简整理得:f(x)=sin(
 +
+ )+
)+ .再
.再 +
+ =kπ(k∈Z),解出x=-
=kπ(k∈Z),解出x=- +
+ kπ,即得函数f(x)图象的对称中心横坐标.
kπ,即得函数f(x)图象的对称中心横坐标.(2)当
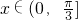 时,可得
时,可得 +
+ ∈(
∈( ,
, ],由此结合正弦函数的图象与性质,即可得到函数当
],由此结合正弦函数的图象与性质,即可得到函数当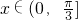 时的值域.
时的值域.点评:本题给出三角函数表达式,求函数图象的对称中心并求闭区间上的值域,着重考查了二倍角的三角函数公式、辅助角公式和正弦函数的图象与性质等知识,属于中档题.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
