题目内容
设F1，F2是椭圆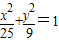
的两焦点，P为椭圆上一点，则三角形PF1F2的周长为（ ）A．16
B．18
C．20
D．不确定
【答案】分析：由已知中椭圆的标准方程，可又求出椭圆的a=5，b=3，c=4，进而根据三角形PF1F2的周长|PF1|+|PF2|+|F1+F2|=2（a+c），可得答案．
解答：解：由椭圆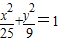
的方程可得
a=5，b=3，c=4
∵F1，F2是椭圆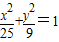
的两焦点，
P为椭圆上一点，
∴三角形PF1F2的周长为|PF1|+|PF2|+|F1+F2|=2（a+c）=18
故选B
点评：本题考查的知识点是椭圆的简单性质，其中根据椭圆上一点到两焦点的距离和为2a，将三角形PF1F2的周长|PF1|+|PF2|+|F1+F2|转化为2（a+c），是解答的关键．
解答：解：由椭圆
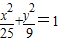的方程可得a=5，b=3，c=4
∵F1，F2是椭圆
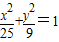的两焦点，P为椭圆上一点，
∴三角形PF1F2的周长为|PF1|+|PF2|+|F1+F2|=2（a+c）=18
故选B
点评：本题考查的知识点是椭圆的简单性质，其中根据椭圆上一点到两焦点的距离和为2a，将三角形PF1F2的周长|PF1|+|PF2|+|F1+F2|转化为2（a+c），是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的两个焦点，P是椭圆上一点，且P到两个焦点的距离之差为2，则△PF1F2是（ ）
的两个焦点，点F1、F2到直线
的距离分别为d1、d2，试求d1·d2的值，并判断直线L与椭圆M的位置关系。
的两个焦点，点F1、F2到直线 
（m、n不同时为0）的距离分别为d1、d2，且直线L与椭圆M相切，试求d1·d2的值。
的两个焦点，以F1为圆心，且过椭圆中心的圆与椭圆的一个交点为M，若直线F2M与圆F1相切，则该椭圆的离心率是 
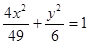的两个焦点，P是椭圆上的点，且
，
的面积为（ ）
D．