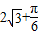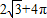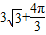题目内容
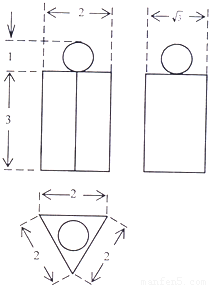
如图为一个几何体的三视图，尺寸如图所示，则该几可体的表面积为（ ）（不考虑接触点）
A．6+
| B．18+
| C．18+2
| D．32+π |
由三视图知，此组合体上部是一个半径为
的球体，故其表面积为π
下部为一直三棱柱，其高为3，底面为一边长为2的正三角形，且题 中已给出此三角形的高为
故三棱柱的侧面积为3×（2+2+2）=18，由于不考虑接触点，故只求上底面的面积即可，
上底面的面积为
×2×
=
故组合体的表面积为18+2
+π
故选C
| 1 |
| 2 |
下部为一直三棱柱，其高为3，底面为一边长为2的正三角形，且题 中已给出此三角形的高为
| 3 |
故三棱柱的侧面积为3×（2+2+2）=18，由于不考虑接触点，故只求上底面的面积即可，
上底面的面积为
| 1 |
| 2 |
| 3 |
| 3 |
故组合体的表面积为18+2
| 3 |
故选C
练习册系列答案
相关题目
（2012•马鞍山二模）如图是一个几何体的三视，则它的表面为（ ）
