Question

已知二次函数y=-x²+mx-1和点A(3,0),B(0,3),求二次函数图像与线段AB有两个不同交点的充要条件.

Answer 1

分析：应先根据图像与线段AB有两个不同交点,导出结论成立的必要条件,即求出m的范围,再证明其为充分条件.

解：(1)必要性:由已知,得线段AB的方程为x+y=3(0≤x≤3),因为二次函数图像与线段AB有两个不同的交点,所以方程组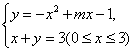有两组不同的实数解.将y=3-x代入y=-x²+mx-1,

得x²-(1+m)x+4=0(0≤x≤3).

令f(x)=x²-(1+m)x+4(如图),

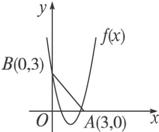
则有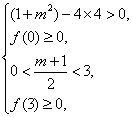

即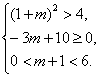

解之,得3＜m≤.

(2)充分性:当3＜m≤时,

x₁==0,

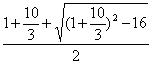x₂=≤=3.

所以方程x²-(1+m)x+4=0有两个不同的实根,且两根x₁,x₂满足0＜x₁＜x₂≤3,即方程组

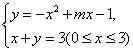有两组不同的实数解.

所以二次函数y=-x²+mx-1和线段AB有两个不同交点的充要条件是3＜m≤.