题目内容
在平行四边形ABCD中,若AC=2且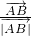 +
+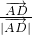 =
=
 ,则
,则 •
• =________.
=________.

分析:由单位向量的意义可知:四边形ABCD和AMHN均为菱形且相似,由此可求得AB和AD的长,在三角形AMH中有余弦定理可得向量夹角的余弦值,由数量积的定义可得答案.
解答:
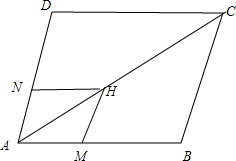 解:(如图)在平行四边形ABCD中,AC=2,
解:(如图)在平行四边形ABCD中,AC=2,设
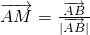 为AB边上的单位向量,
为AB边上的单位向量,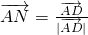 为AC边上的单位向量,且
为AC边上的单位向量,且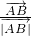 +
+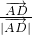 =
=
 =
= ,
,故AC是∠BAD的平分线,四边形ABCD和AMHN均为菱形,且相似.
由题意可得AH=
 =
= ,AB=AD=
,AB=AD=
设向量
 与
与 的夹角大小为θ,在菱形AMHN中,∠AMH=π-θ,AH=
的夹角大小为θ,在菱形AMHN中,∠AMH=π-θ,AH= =
= ,
,△AMH中,由余弦定理可得 3=1+1-2×1×1cos(π-θ)=2+2cosθ,解得 cosθ=
 ,
,故
 •
• =AB×ADcosθ=
=AB×ADcosθ=
故答案为:

点评:本题为向量数量积的求解,结合几何图形求得向量的模长和夹角的余弦值是夹角问题的关键,属中档题.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).
如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).