题目内容
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(1)若不等式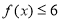 的解集为
的解集为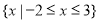 ,求实数
,求实数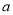 的值;
的值;
(2)在(1)的条件下,若存在实数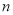 使
使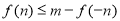 成立,求实数
成立,求实数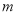 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)理解绝对值的几何意义, 表示的是数轴的上点
表示的是数轴的上点 到原点离;(2)对于恒成立的问题,常用到以下两个结论:(1)
到原点离;(2)对于恒成立的问题,常用到以下两个结论:(1) 恒成立
恒成立 ,(2)
,(2) 恒成立
恒成立
(3) 的应用;(4)掌握一般不等式的解法:
的应用;(4)掌握一般不等式的解法: 或
或 ,
, .
.
试题解析:(1)由 得
得 ,
,
∴ ,即
,即 ,
,
∴
∴ 5分
5分
(2)由(1)知 ,令
,令
则,
∴ 的最小值为4,故实数
的最小值为4,故实数 的取值范围是
的取值范围是 . 10分
. 10分
考点:1、含绝对值不等式的解法;2、恒成立的问题.
考点分析: 考点1:不等式 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,若
中,若 ,
, ,
, 的
的 项和为
项和为 ,则
,则 ( )
( ) B.2 C.
B.2 C. D.
D.
 ,则判断框内应填入的条件是( )
,则判断框内应填入的条件是( )
 B.
B. C.
C. D.
D. 
 的解集为
的解集为 ,则一元一次不等式
,则一元一次不等式 的解集为 .
的解集为 .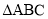 中,角
中,角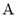 ,
,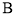 ,
,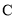 的对边分别为
的对边分别为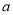 ,
,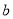 ,
,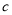 ,且
,且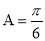 ,
,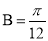 ,
,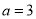 ,则
,则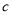 的值为( )
的值为( )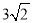 B.
B. C.
C.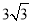 D.
D.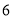
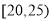 ,第2组
,第2组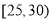 ,第3组
,第3组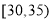 ,第4组
,第4组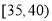 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.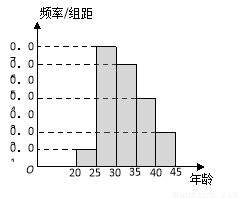
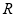 上的可导函数
上的可导函数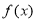 的导函数为
的导函数为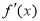 ,若对于任意实数
,若对于任意实数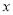 ,有
,有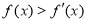 ,且
,且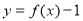 为奇函数,则不等式
为奇函数,则不等式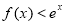 的解集为
的解集为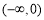 B.
B.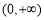 C.
C.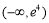 D.
D.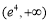
 个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“兰州马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取
个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“兰州马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取 次.已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为
次.已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为 .
. 表示某位嘉宾抽奖的次数,求
表示某位嘉宾抽奖的次数,求 的四个命题:
的四个命题: :
: ,
, 

 的共轭复数为
的共轭复数为
 的虚部为
的虚部为
 B.
B. C.
C. D.
D.