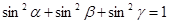题目内容
长方体共顶点的三个面的面积分别是
、
、
,则长方体外接球的表面积是( )
| 2 |
| 3 |
| 6 |
| A、6π | ||
| B、24π | ||
C、
| ||
| D、都不对 |
分析:根据题意建立方程组,解出长方体的长、宽、高分别为
、
、1,从而算出长方体的对角线长l=
,可得外接球的直径R=
,利用球的表面积公式即可算出长方体外接球的表面积.
| 3 |
| 2 |
| 6 |
| ||
| 2 |
解答:解:设长方体的长、宽、高分别为x、y、z,
∵长方体共顶点的三个面的面积分别是
、
、
,
∴
,解之得
,可得长方体的对角线长l=
=
.
设长方体外接球的半径为R,则2R=l=
,可得R=
,
∴长方体外接球的表面积是S=4πR2=4π(
)2=6π.
故选:A
∵长方体共顶点的三个面的面积分别是
| 2 |
| 3 |
| 6 |
∴
|
|
| x2+y2+z2 |
| 6 |
设长方体外接球的半径为R,则2R=l=
| 6 |
| ||
| 2 |
∴长方体外接球的表面积是S=4πR2=4π(
| ||
| 2 |
故选:A
点评:本题给出长方体共顶点的三个面的面积,求外接球的表面积.着重考查了长方体的对角线长公式、矩形面积公式与球的表面积计算等知识,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 ,则
,则 的取值范围为
的取值范围为
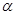 、
、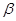 ,则
,则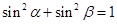 .长方体的一条对角线与三条共顶点的棱所成的角分别为
.长方体的一条对角线与三条共顶点的棱所成的角分别为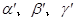 ,与三个共顶点的面所成的角分别为
,与三个共顶点的面所成的角分别为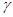 ,用类比推理的方法可知成立的关系式是
,用类比推理的方法可知成立的关系式是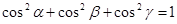 B.
B.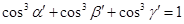 [来源:Zxxk.Com]
[来源:Zxxk.Com]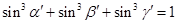 D.
D.