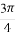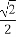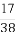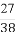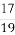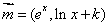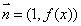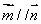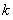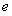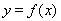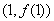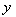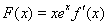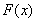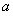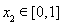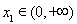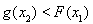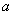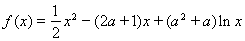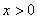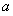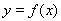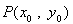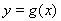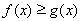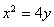题目内容
已知函数
(1)若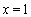 为
为 的极值点,求
的极值点,求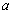 的值;
的值;
(2)若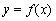 的图象在点
的图象在点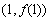 处的切线方程为
处的切线方程为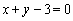 ,
,
①求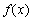 在区间
在区间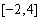 上的最大值;
上的最大值;
②求函数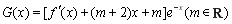 的单调区间.
的单调区间.
⑴ 或2(2)①8②
或2(2)①8② 时,
时, 在
在 单调递减,在
单调递减,在 单调递增;
单调递增; 时,
时, 在
在 单调递减,在
单调递减,在 单调递增.
单调递增.
【解析】⑴ .∵
.∵ 是极值点,
是极值点,
∴ ,即
,即 .∴
.∴ 或2.
或2.
⑵∵ 在
在 上.∴
上.∴
∵ 在
在 上,∴
上,∴
又 ,∴
,∴
∴ ,解得
,解得
∴
①由 可知
可知 和
和 是
是 的极值点.
的极值点.
∵
∴ 在区间
在区间 上的最大值为8.
上的最大值为8.
②

令 ,得
,得
当 时,
时, ,此时
,此时 在
在 单调递减
单调递减
当 时:
时:
|
|
|
| 0 |
|
|
|
| + | 0 |
|
|
| 极小值 |
| 极大值 |
|
此时 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
当 时:
时:
|
| 0 |
|
|
|
|
| 0 | + | 0 |
|
|
| 极小值 |
| 极大值 |
|
此时 在
在 上单调递减,在
上单调递减,在 上单调递增,综上所述:当
上单调递增,综上所述:当 时,
时, 在
在 单调递减;
单调递减;
 时,
时, 在
在 单调递减,在
单调递减,在 单调递增;
单调递增;
 时,
时, 在
在 单调递减,在
单调递减,在 单调递增.
单调递增.

练习册系列答案
相关题目