题目内容
设椭圆| x2 |
| m+1 |
(I)求实数m的取值范围.
(II)设l是相应于焦点F2的准线,直线PF2与l相交于点Q.若
| |QF2| |
| |PF2| |
| 3 |
分析:(1)根据直线PF1⊥直线PF2推断以O为圆心以c为半径的圆与椭圆有交点,两个方程联立,表示出x2,进而根据0≤x2<a2确定m的范围.
(2)设P(x,y),直线PF2方程为:y=k(x-c),根据直线l的方程求得点Q的坐标,根据
=2-
可推断出点P分有向线段
所成比为3-
,进而根据Q和F2的坐标求得点P的坐标,代入椭圆方程求得k,直线PF2的方程可得.
(2)设P(x,y),直线PF2方程为:y=k(x-c),根据直线l的方程求得点Q的坐标,根据
| |QF2| |
| |PF2| |
| 3 |
| QF 2 |
| 3 |
解答:解: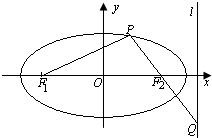 (1)∵直线PF1⊥直线PF2
(1)∵直线PF1⊥直线PF2
∴以O为圆心以c为半径的圆:x2+y2=c2与椭圆:
+y2=1有交点.即
有解
又∵c2=a2-b2=m+1-1=m>0
∴0≤x2=
<a2=m+1
∴m≥1
(2)设P(x,y),直线PF2方程为:y=k(x-c)
∵直线l的方程为:x=
=
∴点Q的坐标为(
,
)
∵
=2-
∴点P分有向线段
所成比为3-
∵F2(
,0),Q(
,
)
∴P(
,
)
∵点P在椭圆上∴
+(
)2=1
∴k=±
直线PF2的方程为:y=±
(x-
).
 (1)∵直线PF1⊥直线PF2
(1)∵直线PF1⊥直线PF2∴以O为圆心以c为半径的圆:x2+y2=c2与椭圆:
| x2 |
| m+1 |
|
又∵c2=a2-b2=m+1-1=m>0
∴0≤x2=
| m2-1 |
| m |
∴m≥1
(2)设P(x,y),直线PF2方程为:y=k(x-c)
∵直线l的方程为:x=
| a2 |
| c |
| m+1 | ||
|
∴点Q的坐标为(
| m+1 | ||
|
| k | ||
|
∵
| |QF2| |
| |PF2| |
| 3 |
∴点P分有向线段
| QF 2 |
| 3 |
∵F2(
| m |
| m+1 | ||
|
| k | ||
|
∴P(
(4-
| ||||
(4-
|
| k | ||||
(4-
|
∵点P在椭圆上∴
(
| ||||||||
| m+1 |
| k | ||||
(4-
|
∴k=±
|
直线PF2的方程为:y=±
|
| m |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目