题目内容
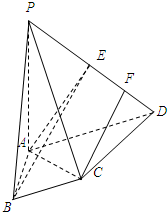 (2008•南京模拟)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥CD,∠DAC=60°,AB=BC=AC,E是PD的中点,F为ED的中点.
(2008•南京模拟)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥CD,∠DAC=60°,AB=BC=AC,E是PD的中点,F为ED的中点.(1)求证:平面PAC⊥平面PCD;
(2)求证:CF∥平面BAE.
分析:(1)由题意可得:PA⊥CD,又AC⊥CD,即可利用线面垂直的判断定理证明线面垂直,进而利用面面垂直的判断定理可得答案.
(2)取AE中点G,连接FG,B G,可得FG∥
AD,再利用解三角形的有关知识可得:BC=
AD,即可得到∠ACB=60°,所以∠ACB=∠DAC,可得四边形FGBC为平行四边形,即
CF∥BG,进而利用线面平行的判断定理可证明线面平行.
(2)取AE中点G,连接FG,B G,可得FG∥
| 1 |
| 2 |
| 1 |
| 2 |
CF∥BG,进而利用线面平行的判断定理可证明线面平行.
解答:证明:(1)因为PA⊥底面ABCD,CD?平面ABCD,
所以PA⊥CD,
又AC⊥CD,且AC∩PA=A,
所以CD⊥平面PAC,…(4分)
又CD?平面PCD,
所以平面PAC⊥平面PCD.…(6分)
(2)取AE中点G,连接FG,B G.
因为F为ED的中点,
所以FG∥
AD.…(8分)
在△ACD中,AC⊥CD,∠DAC=60°,
所以AC=
AD,
所以BC=
AD.
在△ABC中,AB=BC=AC,所以∠ACB=60°,
可得∠ACB=∠DAC,
所以AD∥BC.…(11分)
所以FG∥BC,FG=BC,
所以四边形FGBC为平行四边形,
所以CF∥BG.
又BG?平面BAE,CF?平面BAE,
所以CF∥平面BAE. …(14分)
所以PA⊥CD,
又AC⊥CD,且AC∩PA=A,

所以CD⊥平面PAC,…(4分)
又CD?平面PCD,
所以平面PAC⊥平面PCD.…(6分)
(2)取AE中点G,连接FG,B G.
因为F为ED的中点,
所以FG∥
| 1 |
| 2 |
在△ACD中,AC⊥CD,∠DAC=60°,
所以AC=
| 1 |
| 2 |
所以BC=
| 1 |
| 2 |
在△ABC中,AB=BC=AC,所以∠ACB=60°,
可得∠ACB=∠DAC,
所以AD∥BC.…(11分)
所以FG∥BC,FG=BC,
所以四边形FGBC为平行四边形,
所以CF∥BG.
又BG?平面BAE,CF?平面BAE,
所以CF∥平面BAE. …(14分)
点评:解决此类问题的关键是熟练掌握线面垂直、面面垂直、线面平行的判断定理,以及解三角形的有关知识,此题属于中档题,高考题目的热点之一.

练习册系列答案
相关题目
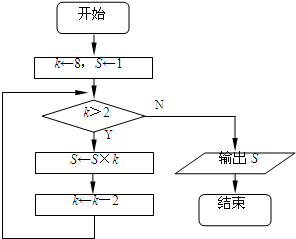 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是