题目内容
某产品40件，其中有次品3件，现从其中任取3件，求取出的3件产品中次品数X的分布列．
X的分布列为
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
解析:
的所有可能取值为0，1，2，3，则服从参数为
的超几何分布．
，
，
，
．
的分布列为
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
某食品厂为了检查甲乙两条自动包装流水线的生产情况，随即在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．图1是甲流水线样本的频率分布直方图，表1是乙流水线样本频数分布表．
某食品厂为了检查甲乙两条自动包装流水线的生产情况，随即在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．图1是甲流水线样本的频率分布直方图，表1是乙流水线样本频数分布表．
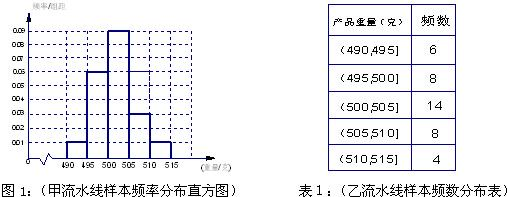
（1）若以频率作为概率，试估计从甲流水线上任取5件产品，求其中合格品的件数X的数学期望；
（2）从乙流水线样本的不合格品中任意取2件，求其中超过合格品重量的件数Y的分布列；
（3）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．
附：下面的临界值表供参考：
（参考公式：K2=
，其中n=a+b+c+d）
（1）若以频率作为概率，试估计从甲流水线上任取5件产品，求其中合格品的件数X的数学期望；
（2）从乙流水线样本的不合格品中任意取2件，求其中超过合格品重量的件数Y的分布列；
（3）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | n= |
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
某糖果厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上40件产品作为样本，它们的质量（单位：克）的分组区间为（990，995]，（995，1000]，…（1010，1015]，由此得到样本的频率分布直方图，如图所示．某产品
40件，其中有次品数3件，现从中任取2件，则其中至少有一件次品的概率是[
]|
A ．0.146 2 |
B ．0.153 8 |
C ．0.996 2 |
D ．0.853 8 |