题目内容
若a,b,c均为正实数,且a,b均不为1,则等式4loga2x+3logb2x=5logax•logbx成立的条件是
x=1
x=1
.分析:令m=logax•n=logbx,将4loga2x+3logb2x=5logax•logbx转化成4m2-5mn+3n2=0,考查方程解的情况作出判断.
解答:解:令m=logax•n=logbx,则4loga2x+3logb2x=5logax•logbx移向整理得,4m2-5mn+3n2=0①
当n=0时,则m=0,此时x=1.
当n≠0时,①式两边同除以n2得 4(
)2-5
+3=0,看作关于
的一元二次方程,△=(-5)2-4×4×3=-23<0,方程无解.
综上所述,只有x=1
故答案为:x=1.
当n=0时,则m=0,此时x=1.
当n≠0时,①式两边同除以n2得 4(
| m |
| n |
| m |
| n |
| m |
| n |
综上所述,只有x=1
故答案为:x=1.
点评:本题考查转化构造、计算能力.利用换元法化成4m2-5mn+3n2=0是关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.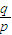 ,其中p、q均为整数且p、q互质)
,其中p、q均为整数且p、q互质)
 ,其中p、q均为整数且p、q互质)
,其中p、q均为整数且p、q互质)