题目内容
已知x1＞0,x1≠1且xn+1=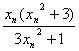
(n=1,2,3,…)，试证：数列{xn}或者对任意n∈N都满足xn＜xn+1，或者对任意n∈N都满足xn＞xn+1.
证明：由于xn+1-xn=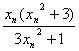-xn=
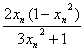且x1＞0,又由题设可知对任意n∈N,有xn＞0,故xn+1-xn与1-xn2同号，于是应分x1＜1与x1＞1两种情况讨论.
（1）若x1＜1,用数归纳法证明1-xn2＞0.
1°当n=1时，1-x12＞0成立.
2°假设当n=k时，1-xk2＞0成立，则当n=k+1时，1-xk+12=1-［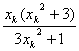
］2=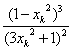
＞0，即当n=k+1时，有1-xk+12＞0成立.故对任意n∈N,都有1-xn2＞0,∴对任意n∈N,有xn+1＞xn.
(2)若x1＞1，同样可证，对任意n∈N,1-xn2＜0,此时有xn+1＜xn.综合（1）、（2），原问题获证.
练习册系列答案
相关题目
x1=logax2=log(a+1)x3＞0,0＜a＜1,则x1、x2、x3的大小关系是( )
[0, 1]，总有f（x）≥0; 
, n
[0, 1]，总有f（x）≥0; 
, n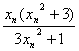
(n=1,2,3,…)，试证：数列{xn}或者对任意n∈N都满足xn＜xn+1，或者对任意n∈N都满足xn＞xn+1.