题目内容
 在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且
在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且
(1)求三角形ABC的面积和边BC的长度;
(2)求sin∠BAD的值.
解:(1)由已知 =13,
=13,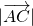 =
= =10,
=10,
 =50?
=50? •
•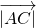 •cos∠BAC=50,
•cos∠BAC=50,
∴cos∠BAC= ,
,
∴sin∠BAC= ,
,
则S△ABC= AB•ACsin∠BAC
AB•ACsin∠BAC
= ×13×10×
×13×10×
=60
由余弦定理得BC= =13
=13
(2)在Rt△CAD中,sin∠CAD= =
=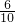 =
= ,cos∠CAD=
,cos∠CAD= =
= ,
,
∴sin∠BAD=sin(∠BAC+∠CAD)
=sin∠BAC•cos∠CAD+cos∠BAC•sin∠CAD
= .
.
分析:(1)由题意可求得cos∠BAC,继而可得sin∠BAC,从而可得S△ABC,再由余弦定理求得BC即可;
(2)在Rt△CAD中,求得sin∠CAD,cos∠CAD,利用两角和的正弦即可求得答案.
点评:本题通过考查平面向量数量积的运算,考查余弦定理及其应用,考查分析与运算的能力,属于中档题.
 =13,
=13,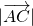 =
= =10,
=10, =50?
=50? •
•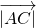 •cos∠BAC=50,
•cos∠BAC=50,∴cos∠BAC=
 ,
,∴sin∠BAC=
 ,
,则S△ABC=
 AB•ACsin∠BAC
AB•ACsin∠BAC=
 ×13×10×
×13×10×
=60
由余弦定理得BC=
 =13
=13(2)在Rt△CAD中,sin∠CAD=
 =
=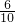 =
= ,cos∠CAD=
,cos∠CAD= =
= ,
,∴sin∠BAD=sin(∠BAC+∠CAD)
=sin∠BAC•cos∠CAD+cos∠BAC•sin∠CAD
=
 .
.分析:(1)由题意可求得cos∠BAC,继而可得sin∠BAC,从而可得S△ABC,再由余弦定理求得BC即可;
(2)在Rt△CAD中,求得sin∠CAD,cos∠CAD,利用两角和的正弦即可求得答案.
点评:本题通过考查平面向量数量积的运算,考查余弦定理及其应用,考查分析与运算的能力,属于中档题.

练习册系列答案
相关题目
 如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则
如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则