题目内容
抛物线C:y=x2上两点M、N满足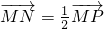 ,若
,若 ,则
,则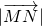 =________.
=________.

分析:首先根据M,N在抛物线上设M(x1,x12),N(x2,x22),,进而表示出向量MN和向量MP,再根据
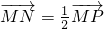 得出以x1=2x2,2x22=-2+x12,即可求出x1和x2,从而求出M,N的坐标,即可得出答案.
得出以x1=2x2,2x22=-2+x12,即可求出x1和x2,从而求出M,N的坐标,即可得出答案.解答:设M(x1,x12),N(x2,x22),则
 =(x2-x1,x22-x12)
=(x2-x1,x22-x12)  =(-x1,-2-x12).
=(-x1,-2-x12).因为
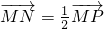 ,
,所以(x2-x1,x22-x12)=
 (-x1,-2-x12),
(-x1,-2-x12),即x2-x1=-
 x1,x22-x12=
x1,x22-x12= (-2-x12),
(-2-x12),所以x1=2x2,2x22=-2+x12,
联立解得:x2=1,x1=2或x2=-1,x1=-2
即M(1,1),N(2,4)或M(-1,1),N(-2,4)
所以|MN|=

故答案为
 .
.点评:本题考查了抛物线的性质以及向量数乘的运算以及几何意义,解题关键是根据向量得出x1=2x2,2x22=-2+x12,属于基础题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目