题目内容
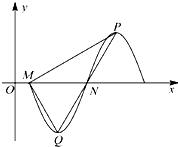
函数y=Acos（ωx+φ），（A＞0，ω＞0）的部分图象如图所示，则f（1）+f（2）+…+f（2010）+f（2011）的值为________．
解：由函数的图象可知A=2，T=8，所以ω=
，因为（0，0）在函数的图象上，所以0=2cos（
φ），φ=
，函数的解析式为：y=2sin
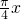，所以f（1）+f（2）+…+f（8）=
+2++0--2--0=0，所以f（1）+f（2）+…+f（2010）+f（2011）=+2+=
故答案为：
分析：通过函数的图象求出A，T确定ω，根据（0，0）在图象上，求出φ，推出函数的解析式，然后确定函数在一个周期内的函数的和值，即可求出f（1）+f（2）+…+f（2010）+f（2011）的值．
点评：本题是基础题，考查三角函数解析式的求法，函数值的求法，周期的应用，考查计算能力，常考题型．
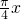，因为（0，0）在函数的图象上，所以0=2cos（φ），φ=，函数的解析式为：y=2sin，所以f（1）+f（2）+…+f（8）=+2++0--2--0=0，所以f（1）+f（2）+…+f（2010）+f（2011）=+2+=故答案为：
分析：通过函数的图象求出A，T确定ω，根据（0，0）在图象上，求出φ，推出函数的解析式，然后确定函数在一个周期内的函数的和值，即可求出f（1）+f（2）+…+f（2010）+f（2011）的值．
点评：本题是基础题，考查三角函数解析式的求法，函数值的求法，周期的应用，考查计算能力，常考题型．
练习册系列答案
相关题目
已知某海滨浴场的海浪高度y（m）是时间t（0≤t≤24，单位：h）的函数，记作y=f（t），下表是某日各时的浪高数据：
经长期观测，y=f（t）的曲线可近似地看成是函数y=Acosωt+b．
（1）求函数y=Acosωt+b的最小正周期T，振幅A及函数表达式．
（2）依据规定：当海浪高度高于1m时才对冲浪爱好者开放，请依据（1）的结论，一天内的上午8：00时至晚上20：00时之间，有多少时间可供冲浪者进行运动．
| t/时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/米 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
（1）求函数y=Acosωt+b的最小正周期T，振幅A及函数表达式．
（2）依据规定：当海浪高度高于1m时才对冲浪爱好者开放，请依据（1）的结论，一天内的上午8：00时至晚上20：00时之间，有多少时间可供冲浪者进行运动．
已知函数y=Acos（