题目内容

设直线l1与l2的方程分别为a1x+b1y+c1=0与a2x+b2y+c2=0，则“a1b2-a2b1=0”是“l1∥l2”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
若a1b2-a2b1=0，不妨设a1=0，b1=1，a2=0，b2=1，c1=c2，此时两直线重合，所以不充分．
若l1∥l2，则必有a1b2-a2b1=0成立．
所以“a1b2-a2b1=0”是“l1∥l2”的必要不充分条件．
故选B．
练习册系列答案
相关题目
（2013•揭阳一模）如图，设点F1（-c，0）、F2（c，0）分别是椭圆C：
x2
a2
+y2=1(a＞1)的左、右焦点，P为椭圆C上任意一点，且
PF1
•
PF2
最小值为0．
（1）求椭圆C的方程；
（2）设直线l1：y=kx+m，l2：y=kx+n，若l1、l2均与椭圆C相切，证明：m+n=0；
（3）在（2）的条件下，试探究在x轴上是否存在定点B，点B到l1，l2的距离之积恒为1？若存在，请求出点B坐标；若不存在，请说明理由．
已知中心在坐标原点、焦点在x轴上椭圆的离心率e=
3
3
，以原点为圆心，椭圆的短半轴长为半径的圆与直线y=x+2相切．
（1）求该椭圆的标准方程；
（2）设椭圆的左，右焦点分别是F1和F2，直线l1过F2且与x轴垂直，动直线l2与y轴垂直，l2交l1于点P，求线段PF1的垂直平分线与l2的交点M的轨迹方程，并指明曲线类型．

如图，设点F1（-c，0）、F2（c，0）分别是椭圆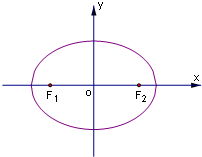数学公式的左、右焦点，P为椭圆C上任意一点，且数学公式最小值为0．
（1）求椭圆C的方程；
（2）设直线l1：y=kx+m，l2：y=kx+n，若l1、l2均与椭圆C相切，证明：m+n=0；
（3）在（2）的条件下，试探究在x轴上是否存在定点B，点B到l1，l2的距离之积恒为1？若存在，请求出点B坐标；若不存在，请说明理由．
如图，设点F1（-c，0）、F2（c，0）分别是椭圆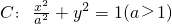的左、右焦点，P为椭圆C上任意一点，且最小值为0．
（1）求椭圆C的方程；
（2）设直线l1：y=kx+m，l2：y=kx+n，若l1、l2均与椭圆C相切，证明：m+n=0；
（3）在（2）的条件下，试探究在x轴上是否存在定点B，点B到l1，l2的距离之积恒为1？若存在，请求出点B坐标；若不存在，请说明理由．
已知中心在坐标原点、焦点在x轴上椭圆的离心率，以原点为圆心，椭圆的短半轴长为半径的圆与直线y=x+2相切．
（1）求该椭圆的标准方程；
（2）设椭圆的左，右焦点分别是F1和F2，直线l1过F2且与x轴垂直，动直线l2与y轴垂直，l2交l1于点P，求线段PF1的垂直平分线与l2的交点M的轨迹方程，并指明曲线类型．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网