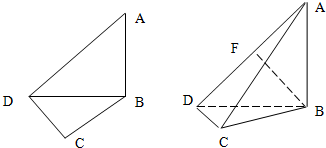
题目内容
如图,将平面四边形ABCD,沿AC折成空间四边形,当平面四边形满足_________时,空间四边形中的两条对角线互相垂直.(填上你认为正确的一种条件即可,不必考虑所有可能情况)
解析:在平面四边形中,设AC与BD交于E,假设AC⊥BD,则AC⊥DE,AC⊥BE.折叠后,AC与DE,AC与BE依然垂直,所以AC⊥平面BDE.所以AC⊥BD.
若四边形ABCD为菱形或正方形,因为它们的对角线互相垂直,仿上可证AC⊥BD.
答案:AC⊥BD(或ABCD为菱形,正方形等.答案不唯一).
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
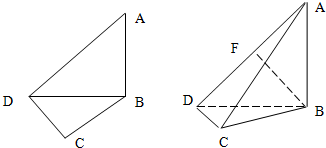如图，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC，设点F为棱AD的中点．
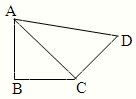如图，在平面四边形ABCD中，AB=BC=CD=a，∠ABC=90°，∠BCD=135°，沿对角线AC将此四边形折成直二面角．
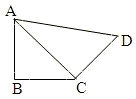如图，在平面四边形ABCD中，AB=BC=CD=a，∠ABC=90°，∠BCD=135°，沿对角线AC将此四边形折成直二面角．
