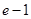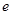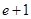题目内容
(本小题满分14分)
已知函数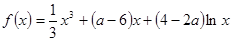 ,
,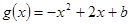
(Ⅰ)若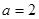 ,求
,求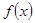 的单调区间;
的单调区间;
(Ⅱ)在(Ⅰ)的条件下,对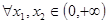 ,都有
,都有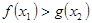 ,求实数
,求实数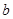 的取值范围;
的取值范围;
(Ⅲ)若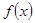 在
在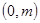 ,
,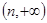 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数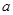 的取值范围。
的取值范围。
已知函数
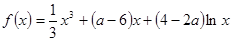 ,
,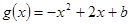
(Ⅰ)若
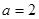 ,求
,求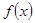 的单调区间;
的单调区间;(Ⅱ)在(Ⅰ)的条件下,对
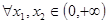 ,都有
,都有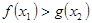 ,求实数
,求实数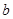 的取值范围;
的取值范围;(Ⅲ)若
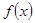 在
在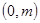 ,
,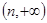 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数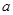 的取值范围。
的取值范围。(Ⅰ) 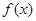 的递减区间为(0,2),递增区间为
的递减区间为(0,2),递增区间为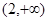 ;
;
(Ⅱ)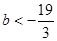 ;(Ⅲ)
;(Ⅲ)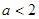 且
且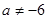 。
。
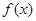 的递减区间为(0,2),递增区间为
的递减区间为(0,2),递增区间为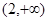 ;
;(Ⅱ)
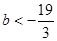 ;(Ⅲ)
;(Ⅲ)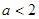 且
且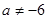 。
。本试题主要是考查了导数在研究函数中的运用。
(1)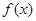 定义域为
定义域为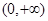
当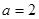 时,
时,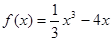 ,
,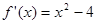 ,令
,令 得
得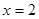 或
或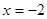 (舍)
(舍)
求解函数的单调区间。
(2)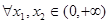 都有
都有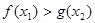 成立
成立
∴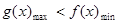 ,可以求解得到。
,可以求解得到。
(3) 因为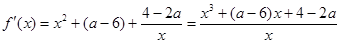
由条件知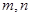 恰为
恰为 的两个不相等正根,即
的两个不相等正根,即 恰有两个不相等正根。
恰有两个不相等正根。
解:(Ⅰ)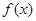 定义域为
定义域为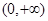
当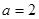 时,
时,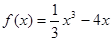 ,
,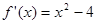 ,令
,令 得
得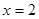 或
或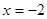 (舍)
(舍)
∴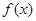 的递减区间为(0,2),递增区间为
的递减区间为(0,2),递增区间为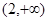 …………………4分
…………………4分
(Ⅱ)∵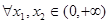 都有
都有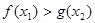 成立
成立
∴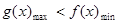 ……………………5分
……………………5分
由(Ⅰ)知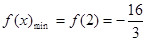
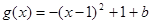 ,
,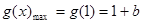 …………………7分
…………………7分
∴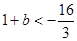 ,∴
,∴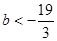 …………………………………8分
…………………………………8分
(Ⅲ)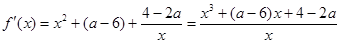 ………………9分
………………9分
由条件知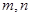 恰为
恰为 的两个不相等正根,
的两个不相等正根,
即 恰有两个不相等正根,………………10分
恰有两个不相等正根,………………10分
对于方程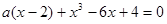 显然
显然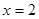 是方程的一个解,………………11分
是方程的一个解,………………11分
当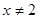 时,
时,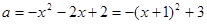 (
(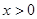 且
且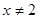 )
)
当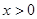 时,
时,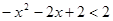
当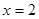 时,
时,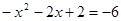 ……………………………13分
……………………………13分
∴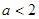 且
且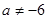 ………………………14分
………………………14分
(1)
 定义域为
定义域为
当
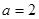 时,
时,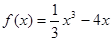 ,
,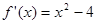 ,令
,令 得
得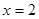 或
或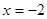 (舍)
(舍)求解函数的单调区间。
(2)
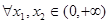 都有
都有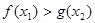 成立
成立∴
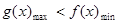 ,可以求解得到。
,可以求解得到。(3) 因为
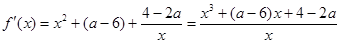
由条件知
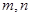 恰为
恰为 的两个不相等正根,即
的两个不相等正根,即 恰有两个不相等正根。
恰有两个不相等正根。解:(Ⅰ)
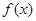 定义域为
定义域为
当
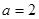 时,
时,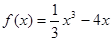 ,
,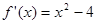 ,令
,令 得
得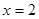 或
或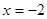 (舍)
(舍)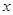 | (0,2) | 2 | 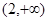 |
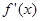 | - | 0 | + |
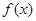 | ↘ | | ↗ |
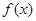 的递减区间为(0,2),递增区间为
的递减区间为(0,2),递增区间为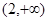 …………………4分
…………………4分(Ⅱ)∵
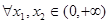 都有
都有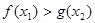 成立
成立∴
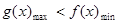 ……………………5分
……………………5分由(Ⅰ)知
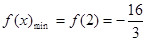
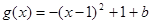 ,
,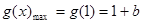 …………………7分
…………………7分∴
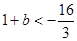 ,∴
,∴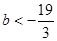 …………………………………8分
…………………………………8分(Ⅲ)
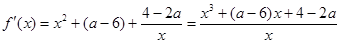 ………………9分
………………9分由条件知
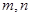 恰为
恰为 的两个不相等正根,
的两个不相等正根,即
 恰有两个不相等正根,………………10分
恰有两个不相等正根,………………10分对于方程
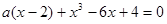 显然
显然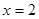 是方程的一个解,………………11分
是方程的一个解,………………11分当
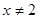 时,
时,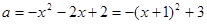 (
(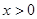 且
且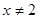 )
)当
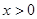 时,
时,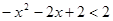
当
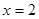 时,
时,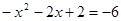 ……………………………13分
……………………………13分∴
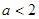 且
且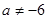 ………………………14分
………………………14分
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
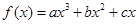 的极小值为
的极小值为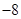 ,其导函数
,其导函数 的图像开口向下且经过点
的图像开口向下且经过点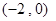 ,
,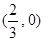 .
.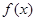 的解析式;(Ⅱ)方程
的解析式;(Ⅱ)方程 有唯一实数解,求
有唯一实数解,求 的取值范围.
的取值范围. 都有
都有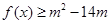 恒成立,求实数
恒成立,求实数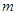 的取值范围.
的取值范围.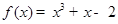 在
在 处的切线平行于直线
处的切线平行于直线 ,则
,则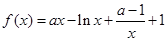 .
.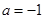 时,求曲线
时,求曲线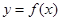 在点
在点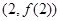 处的切线方程;
处的切线方程;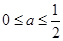 时,讨论
时,讨论 的单调性.
的单调性.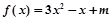 ,
,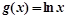 ,若函数
,若函数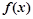 与
与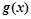 的图象在
的图象在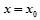 处的切线平行,则
处的切线平行,则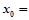 .
. 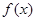 满足:①在x=1时有极值;②图像过点
满足:①在x=1时有极值;②图像过点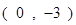 ,且在该点处的切线与直线
,且在该点处的切线与直线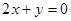 平行.
平行.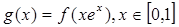 的值域;
的值域; 上任意两点的连线的斜率恒大于
上任意两点的连线的斜率恒大于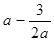 ,求
,求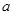 的取值范围.
的取值范围.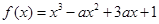 在区间
在区间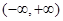 内既有极大值,又有极小值,
内既有极大值,又有极小值, 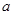 的取值范围是 .
的取值范围是 .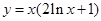 在点(1,1)处的切线方程是____________________
在点(1,1)处的切线方程是____________________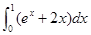 等于( )
等于( )