Question

已知函数f(x)是(－∞，＋∞)上的增函数，a，b∈R．

(1)若a＋b≥0，求证：f(a)＋f(b)≥f(－a)＋f(－b)；

(2)判断(1)中命题的逆命题是否成立，并证明你的结论．

 

Answer 1

【答案】

(1) 证明：∵a＋b≥0，∴a≥－b. 由f(x)的单调性得f(a)≥f(－b) 又a＋b≥0?b≥－a?f(b)≥f(－a) 两式相加即得：f(a)＋f(b)≥f(－a)＋f(－b) (2) 逆命题成立，假设a＋b<0，那么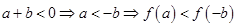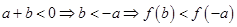，?f(a)＋f(b)<f(－a)＋f(－b) 这与已知矛盾，故只有a＋b≥0

【解析】

试题分析：(1)证明：∵a＋b≥0，∴a≥－b.           2分

由已知f(x)的单调性得f(a)≥f(－b)．

又a＋b≥0?b≥－a?f(b)≥f(－a)．         4分

两式相加即得：f(a)＋f(b)≥f(－a)＋f(－b)．         6分

(2)逆命题：

f(a)＋f(b)≥f(－a)＋f(－b)?a＋b≥0.           8分

下面用反证法证之．

假设a＋b<0，那么：

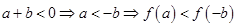
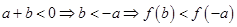
?f(a)＋f(b)<f(－a)＋f(－b)．          10分

这与已知矛盾，故只有a＋b≥0.逆命题得证．          12分

考点：函数单调性与反证法

点评：单调性的定义：在定义域的某个区间上，若有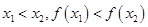则函数为增函数，若有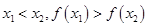则函数为减函数；反证法证明的大体步骤：假设要证明的结论反面成立，借此推出与已知或定理发生矛盾，推翻假设肯定原结论成立