题目内容
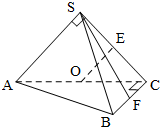 如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=| 2 |
| 1 |
| 2 |
(Ⅰ)求证:OE⊥平面SBC;
(Ⅱ)若点F为线段BC的中点,求异面直线SF与AB所成角的正切值.
分析:(Ⅰ)根据线面垂直的判定定理证明OE⊥平面SBC;
(Ⅱ)根据异面直线的定义求出异面直线的所成的角,然后三角形的边角关系求正切值即可.
(Ⅱ)根据异面直线的定义求出异面直线的所成的角,然后三角形的边角关系求正切值即可.
解答:解:(Ⅰ)∵E,O分别是SC,AC的中点,∴EO∥SA ①
∵∠ACB=90°,∴BC⊥AC,∠ASC=90°,∴SC⊥SA,
∵平面SAC⊥平面ABC,
∴BC⊥平面SAC,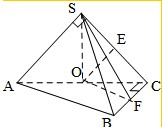
∵SA?平面SAC,
∴BC⊥SA,
又SA⊥SC,BC∩SC=C,
∴SA⊥平面SBC ②,
由①②知OE⊥平面SBC.
(Ⅱ)连接OF,OS,
∵O,F是AC,BC的中点,
∴OF∥AB且OF=
AB,
∴∠OFS是异面直线SF与AB所成的角.
等腰直角三角形SAC中AC=
=2,且SO=1,SO⊥AC,
又平面SAC⊥平面ABC,
∴SO⊥平面ABC,
∵OF?平面ABC,
∴S0⊥OF,
∴OF=
AB=
=
,
∴tan∠SFO=
=
.
∵∠ACB=90°,∴BC⊥AC,∠ASC=90°,∴SC⊥SA,
∵平面SAC⊥平面ABC,
∴BC⊥平面SAC,

∵SA?平面SAC,
∴BC⊥SA,
又SA⊥SC,BC∩SC=C,
∴SA⊥平面SBC ②,
由①②知OE⊥平面SBC.
(Ⅱ)连接OF,OS,
∵O,F是AC,BC的中点,
∴OF∥AB且OF=
| 1 |
| 2 |
∴∠OFS是异面直线SF与AB所成的角.
等腰直角三角形SAC中AC=
| SA2+SC2 |
又平面SAC⊥平面ABC,
∴SO⊥平面ABC,
∵OF?平面ABC,
∴S0⊥OF,
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
| AB2+BC2 |
| ||
| 2 |
∴tan∠SFO=
| SO |
| OF |
2
| ||
| 5 |
点评:本题主要考查直线和平面垂直的判断以及异面直线所成角的求法,要求熟练掌握线面垂直的判定定理以及异面直线所成角的定义和求法.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC. 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( ) 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( ) (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )