Question

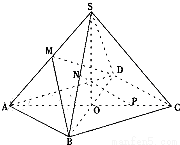
在正四棱锥S-ABCD中，点E是BC的中点，动点P在侧面SCD内运动，且总有PE⊥AC，则动点P的轨迹是

1. A.
   SC的中点
2. B.
   点S与CD中点的连线
3. C.
   线段SC
4. D.
   SC的中点与CD的中点的连线

Answer 1

D
分析：设AC、BD交于点O，SC、CD的中点分别为M、N，连接SO、MN、EM、EN．由正四棱锥的性质，证出AC⊥平面SBD，得AC⊥SD，结合MN∥SD可得AC⊥MN．正方形ABCD中证出AC⊥NE，从而得到AC⊥平面MNE，因此经过点E与AC垂直的直线总在平面EMN内，由此可得动点P的轨迹对应的图形．
解答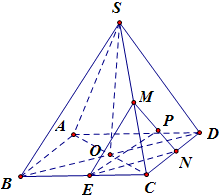：解：设AC、BD交于点O，SC的中点为M，CD的中点为N，连接SO、MN、EM、EN
∵AC⊥BD，AC⊥SO，BD、SO是平面SBD内的相交直线
∴AC⊥平面SBD，可得AC⊥SD
∵MN是△SCD的中位线，∴MN∥SD可得AC⊥MN，
又∵正方形ABCD中，E、N分别为BC、CD的中点
∴AC⊥NE，
∵EN、MN是平面EMN内的相交直线，
∴AC⊥平面MNE，
因此不论P在线段MN的何处总有PE⊥AC，即动点P的轨迹是SC的中点与CD的中点的连线．
故选：D
点评：本题给出正四棱锥S-ABCD，求经过BC中点E与AC垂直的平面与平面SCD的交线．着重考查了线面垂直的判定与性质和正四棱锥的性质等知识，属于基础题．