题目内容
设函数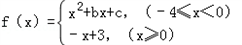 ,若f(﹣4)=f(0),f(﹣2)=﹣1,
,若f(﹣4)=f(0),f(﹣2)=﹣1,
(1)求函数f(x)的解析式,
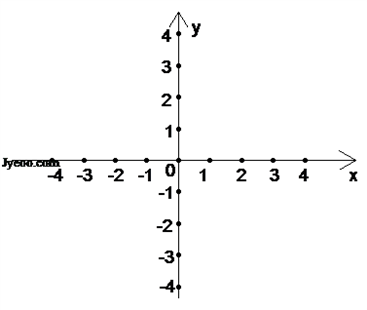
(2)画出函数f(x)的图象,并指出函数的定义域和值域.
(3)解不等式xf(x)<0.
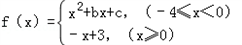 ,若f(﹣4)=f(0),f(﹣2)=﹣1,
,若f(﹣4)=f(0),f(﹣2)=﹣1,(1)求函数f(x)的解析式,
(2)画出函数f(x)的图象,并指出函数的定义域和值域.
(3)解不等式xf(x)<0.
解:(1)∵f(-4)=f(0),f(-2)=-1,
∴16﹣4b+c=3,4-2b+c=﹣1
解得:b=4,c=3
∴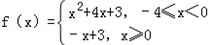
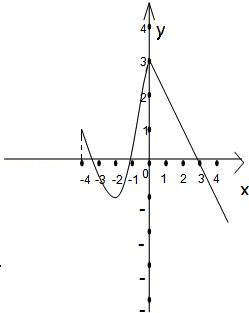
(2)图象见下所示,
由图象可知:函数的定义域:[﹣4,+∞)值域:(﹣∞,3].(3)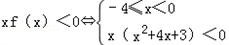 或
或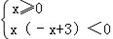 .
.
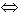 -4≤x<-3或-1<x<0或x>3
-4≤x<-3或-1<x<0或x>3
∴不等式xf(x)<0解集为{x|﹣4≤x<-3或-1<x<0或x>3}
∴16﹣4b+c=3,4-2b+c=﹣1
解得:b=4,c=3
∴
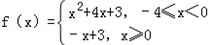
(2)图象见下所示,
由图象可知:函数的定义域:[﹣4,+∞)值域:(﹣∞,3].(3)
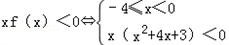 或
或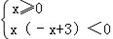 .
.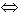 -4≤x<-3或-1<x<0或x>3
-4≤x<-3或-1<x<0或x>3∴不等式xf(x)<0解集为{x|﹣4≤x<-3或-1<x<0或x>3}


练习册系列答案
相关题目
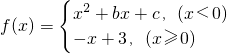 ,若f(-4)=f(0),f(-2)=-1,
,若f(-4)=f(0),f(-2)=-1, ,若f(-4)=f(0),f(-2)=-2,则函数g(x)=f(x)-x的零点个数为 .
,若f(-4)=f(0),f(-2)=-2,则函数g(x)=f(x)-x的零点个数为 . ,若f(-4)=f(0),f(-2)=-1,
,若f(-4)=f(0),f(-2)=-1, ,若f(4)=f(0),f(2)=2,则函数g(x)=f(x)-x的零点的个数是( )
,若f(4)=f(0),f(2)=2,则函数g(x)=f(x)-x的零点的个数是( ) ,若f(4)=f(0),f(2)=2,则函数g(x)=f(x)-x的零点的个数是( )
,若f(4)=f(0),f(2)=2,则函数g(x)=f(x)-x的零点的个数是( )