Question

已知函数f(x)=x+

a

x

+b(x≠0)，其中a，b∈R．
（Ⅰ）若曲线y=f（x）在点P（2，f（2））处的切线方程为y=3x+1，求函数f（x）的解析式；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）若对于任意的a∈[

1

2

，2]，不等式f（x）≤10在[

1

4

，1]上恒成立，求b的取值范围．

Answer 1

（Ⅰ）f′(x)=1-

a

x2

，由导数的几何意义得f'（2）=3，于是a=-8．
由切点P（2，f（2））在直线y=3x+1上可得-2+b=7，解得b=9．
所以函数f（x）的解析式为f(x)=x-

8

x

+9．
（Ⅱ）f′(x)=1-

a

x2

．
当a≤0时，显然f'（x）＞0（x≠0）．这时f（x）在（-∞，0），（0，+∞）上内是增函数．
当a＞0时，令f'（x）=0，解得x=±

a

．
当x变化时，f'（x），f（x）的变化情况如下表：



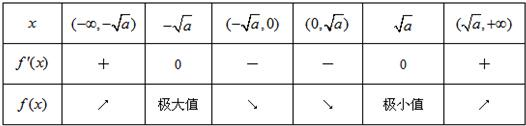
所以f（x）在(-∞，-

a

)，(

a

，+∞)内是增函数，在(-

a

，0)，（0，+∞）内是减函数．
（Ⅲ）由（Ⅱ）知，f（x）在[

1

4

，1]上的最大值为f(

1

4

)与f（1）的较大者，对于任意的a∈[

1

2

，2]，不等式f（x）≤10在[

1

4

，1]上恒成立，当且仅当

f( 1 4 )≤10 f(1)≤10

，
即

b≤ 39 4 -4a b≤9-a

，对任意的a∈[

1

2

，2]成立．
从而得b≤

7

4

，所以满足条件的b的取值范围是(-∞，

7

4

]．