Question

已知x，y满足

x-y+2≥0 x+y-2≤0 0≤y＜2

，(x∈Z，y∈Z)，每一对整数（x，y）对应平面上一个点，则过这些点中的其中3个点可作不同的圆的个数为（　　）

• A、45
• B、36
• C、30
• D、27

Answer 1

分析：画出可行域，找出可行域中的整数点，利用组合数求出所有的取三点的方法，再减去共直线不能共圆的，和四点共圆的重复情况即可．

解答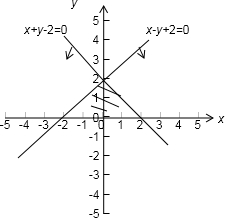：解：作出不等式组

x-y+2≥0 x+y-2≤0 0≤y＜2

，(x∈Z，y∈Z)可行域
可行域中所有的整数点有（-2，0），（-1，0），（0，0），（1，0），（2，0），（-1，1），（0，1），（1，1）；
经过其中任意不共线的三点作直线可作不同的圆，则可作不同的圆的个数是：C₈³-C₅³-C₃³=45．
再减去其中四点共圆的情况，共5种情况
∴符合题意的情况共有45-4C₄³+5=30．
故选：C

点评：求完成某事件的方法数常用的方法是排列、组合的方法有时还用列举的方法．