题目内容
设函数 在区间(0,+∞)内有零点,则实数a的取值范围是
在区间(0,+∞)内有零点,则实数a的取值范围是
- A.(0,+∞)
- B.(-∞,1]
- C.[1,+∞)
- D.[2,+∞)
C
分析:对于函数 ,令t=
,令t= ,由基本不等式可得t的最小值为2,结合对数函数的性质,可得f(x)的最小值为1-a,由函数的零点的定义,分析可得若f(x)在区间(0,+∞)内有零点,必有1-a≤0,解可得a的范围,即可得答案.
,由基本不等式可得t的最小值为2,结合对数函数的性质,可得f(x)的最小值为1-a,由函数的零点的定义,分析可得若f(x)在区间(0,+∞)内有零点,必有1-a≤0,解可得a的范围,即可得答案.
解答:对于函数 ,
,
令t= ,则t=x+
,则t=x+ ,(x>0)
,(x>0)
当x>0时,易得t≥2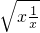 =2,即t有最小值2,
=2,即t有最小值2,
此时有f(x)≥log22-a=1-a,即f(x)在区间(0,+∞)上有最小值1-a,
若其在区间(0,+∞)内有零点,
必有1-a≤0,即a≥1;
故选C.
点评:本题考查函数的零点判定与基本不等式的应用,关键是利用对数函数的性质与基本不等式,求出函数的最小值.
分析:对于函数
 ,令t=
,令t= ,由基本不等式可得t的最小值为2,结合对数函数的性质,可得f(x)的最小值为1-a,由函数的零点的定义,分析可得若f(x)在区间(0,+∞)内有零点,必有1-a≤0,解可得a的范围,即可得答案.
,由基本不等式可得t的最小值为2,结合对数函数的性质,可得f(x)的最小值为1-a,由函数的零点的定义,分析可得若f(x)在区间(0,+∞)内有零点,必有1-a≤0,解可得a的范围,即可得答案.解答:对于函数
 ,
,令t=
 ,则t=x+
,则t=x+ ,(x>0)
,(x>0)当x>0时,易得t≥2
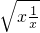 =2,即t有最小值2,
=2,即t有最小值2,此时有f(x)≥log22-a=1-a,即f(x)在区间(0,+∞)上有最小值1-a,
若其在区间(0,+∞)内有零点,
必有1-a≤0,即a≥1;
故选C.
点评:本题考查函数的零点判定与基本不等式的应用,关键是利用对数函数的性质与基本不等式,求出函数的最小值.

练习册系列答案
相关题目
 在区间(0,4)上是减函数,则
在区间(0,4)上是减函数,则 的取值范围是( )
的取值范围是( )
 B.
B.

 D.
D.

 在区间(0,4)上是减函数,则
在区间(0,4)上是减函数,则 的取值范围是 ( )
的取值范围是 ( )  B.
B. C.
C. D.
D.
 在区间(0,4)上是减函数,则k的取值范围( )
在区间(0,4)上是减函数,则k的取值范围( ) B、
B、 C、
C、 D、
D、
 在区间(0,+∞)内有零点,则实数a的取值范围是( )
在区间(0,+∞)内有零点,则实数a的取值范围是( )