题目内容
若直线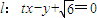
与曲线C：x2-y2=2有两个不同交点，则实数t的取值范围是 ．
【答案】分析：直线方程即y=tx+
，代入曲线C：x2-y2=2化简可得 （1-t2）x2+2
tx-8=0有两个不同的解，故有 
，由此求得 实数t的取值范围．
解答：解：直线方程即 y=tx+
，代入曲线C：x2-y2=2化简可得 （1-t2）x2+2
tx-8=0．
由题意可得，此方程有两个不同的解，故有
，即 
．
∴实数t的取值范围是 （-2，-1）∪（-1，1）∪（1，2），
故答案为（-2，-1）∪（-1，1）∪（1，2）．
点评：本题考查直线和圆锥曲线的位置关系，一元二次方程有两个解的条件，得到
，是解题的关键．
，代入曲线C：x2-y2=2化简可得 （1-t2）x2+2tx-8=0有两个不同的解，故有 ，由此求得 实数t的取值范围．解答：解：直线方程即 y=tx+
，代入曲线C：x2-y2=2化简可得 （1-t2）x2+2tx-8=0．由题意可得，此方程有两个不同的解，故有
，即 ．∴实数t的取值范围是 （-2，-1）∪（-1，1）∪（1，2），
故答案为（-2，-1）∪（-1，1）∪（1，2）．
点评：本题考查直线和圆锥曲线的位置关系，一元二次方程有两个解的条件，得到
，是解题的关键． 
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
已知曲线C：
-
=1，下列叙述中错误的是（ ）
| x|x| |
| a2 |
| y|y| |
| b2 |
| A、垂直于x轴的直线与曲线C只有一个交点 | ||
| B、直线y=kx+m（k，m∈R）与曲线C最多有三个交点 | ||
| C、曲线C关于直线y=-x对称 | ||
D、若P1（x1，y1），P2（x2，y2）为曲线C上任意两点，则有
|
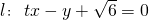与曲线C：x2-y2=2有两个不同交点，则实数t的取值范围是________．