题目内容
已知数列{an}的前n项和Sn= n(n+1)(n+2),试求数列
n(n+1)(n+2),试求数列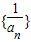 的前n项和.
的前n项和.
【答案】分析:由数列的前n项和求出数列的通项,然后利用列项相消法求数列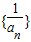 的前n项和.
的前n项和.
解答:解:由Sn= n(n+1)(n+2),
n(n+1)(n+2),
当n=1时,a1=S1=2.
当n≥2时,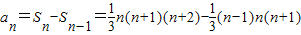 =n(n+1).
=n(n+1).
当n=1时上式成立,所以an=n(n+1).
则数列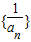 的前n项和为:
的前n项和为:
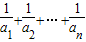 =
=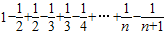
=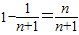 .
.
点评:本题考查了由数列的前n项和求数列的通项,考查了裂项相消法求数列的和,是基础题.
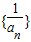 的前n项和.
的前n项和.解答:解:由Sn=
 n(n+1)(n+2),
n(n+1)(n+2),当n=1时,a1=S1=2.
当n≥2时,
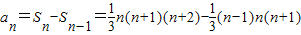 =n(n+1).
=n(n+1).当n=1时上式成立,所以an=n(n+1).
则数列
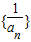 的前n项和为:
的前n项和为: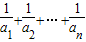 =
=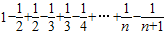
=
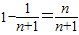 .
.点评:本题考查了由数列的前n项和求数列的通项,考查了裂项相消法求数列的和,是基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |