题目内容
16．
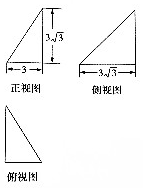已知某几何体的三视图如图所示，则该几何体的内切球的体积为（ ）| A． | $\frac{1}{4}$π | B． | $\frac{\sqrt{3}}{4}$π | C． | $\frac{1}{2}$π | D． | $\frac{\sqrt{3}}{2}$π |
分析 由三视图，可得直观图是有一侧棱垂直于底面的三棱锥，底面为直角边长分别为3，3$\sqrt{3}$的直角三角形，三棱锥的高为3$\sqrt{3}$，利用等体积方法求出内切球的半径，即可求出该几何体的内切球的体积．
解答 解：由三视图，可得直观图是有一侧棱垂直于底面的三棱锥，底面为直角边长分别为3，3$\sqrt{3}$的直角三角形，三棱锥的高为3$\sqrt{3}$，体积为$\frac{1}{3}×\frac{1}{2}×3×3\sqrt{3}×3\sqrt{3}$=$\frac{27}{2}$，三棱锥的表面积为2×$\frac{1}{2}×3×3\sqrt{3}$+$\frac{1}{2}×\sqrt{27+9}×3\sqrt{3}$×2=27$\sqrt{3}$，
设内切球的半径为r，则$\frac{1}{3}×27\sqrt{3}×r=\frac{27}{2}$，∴r=$\frac{\sqrt{3}}{2}$，
∴该几何体的内切球的体积为$\frac{4}{3}π•（\frac{\sqrt{3}}{2}）^{3}$=$\frac{\sqrt{3}}{2}π$，
故选D．
点评 本题考查了由三视图求几何体的面积体积的问题，注意三视图中：正侧一样高，正俯一样长，俯侧一样宽．
练习册系列答案
相关题目
16．如图是求样本x1，x2，…，x10平均数$\overline x$的程序框图，图中空白框中应填入的内容为（ ）
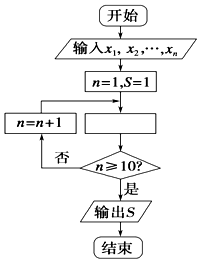
| A． | $S=S+\frac{x_n}{10}$ | B． | $S=S+\frac{x_n}{n}$ | C． | S=S+n | D． | S=S+xn |
7．已知cos（θ+$\frac{π}{2}$）=$\frac{4}{5}$，-$\frac{π}{2}$＜θ＜$\frac{π}{2}$，则sin2θ的值等于（ ）
| A． | -$\frac{24}{25}$ | B． | $\frac{24}{25}$ | C． | -$\frac{12}{25}$ | D． | $\frac{12}{25}$ |
4．若数列{an}满足（2n+3）an+1-（2n+5）an=（2n+3）（2n+5）lg（1+$\frac{1}{n}$），且a1=5，则数列{$\frac{{a}_{n}}{2n+3}$}的第2016项为（ ）
| A． | lg2017 | B． | lg2016 | C． | 1+lg2016 | D． | 1+lg2017 |
8．有一段演绎推理：“直线平行于平面，则这条直线平行于平面内所有直线；已知直线b?平面α，直线a?平面α，直线b∥平面α，则直线b∥直线a”的结论是错误的，这是因为（ ）
| A． | 大前提错误 | B． | 小前提错误 | C． | 推理形式错误 | D． | 非以上错误 |
5．一个几何体的三视图，则它的体积为（ ）
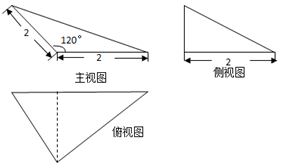
| A． | $\frac{2}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | 2$\sqrt{3}$ | D． | $\frac{2\sqrt{3}}{3}$ |