题目内容
若离散型随机变量X的分布表如右图所示，则常数c=| X | 0 | 1 |
| P | 9c2-c | 3-8c |
分析：根据分布列中所有的概率之和等于1，得到关于c的一元二次方程，解方程得到两个值，把这两个值代入验证去掉不合题意的数字．
解答：解：根据分布列的性质可以得到9c2-c+3-8c=1
∴9c2-9c+2=0
∴c=
，c=
当c=
时3-8c＜0，
不合题意，
故答案为：
∴9c2-9c+2=0
∴c=
| 2 |
| 3 |
| 1 |
| 3 |
当c=
| 2 |
| 3 |
不合题意，
故答案为：
| 1 |
| 3 |
点评：本题考查离散型随机变量的分布列的性质，本题解题的关键是一定要舍去不合题意的结果，注意抓住分布列的性质．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
以下四个命题：
①由圆的过圆心的弦最长的性质类比出球的过球心的截面面积最大的性质；
②若（3x-1）7=a7x7+a6x6+…+a1x+a0，则a7+a6+…+a1=129；
③在含有5件次品的100件产品中，任取3件，则取到两件次品的概率为
；
④若离散型随机变量X的方差为D（X）=2，则D（2X-1）=8．
其中正确命题的序号是（ ）
①由圆的过圆心的弦最长的性质类比出球的过球心的截面面积最大的性质；
②若（3x-1）7=a7x7+a6x6+…+a1x+a0，则a7+a6+…+a1=129；
③在含有5件次品的100件产品中，任取3件，则取到两件次品的概率为
| ||||
|
④若离散型随机变量X的方差为D（X）=2，则D（2X-1）=8．
其中正确命题的序号是（ ）
| A、①②④ | B、①②③④ |
| C、①② | D、①③④ |
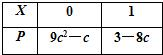若离散型随机变量X的分布列如图，则常数c的值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
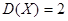，则
；
；
，则
．
；