题目内容
奇函数f (x)的定义域为R,且在[0,+∞]上是增函数,是否存在实数m,使f (2t2-4)+f (4m-2mt)>f (0)对一切t∈[0,1]均成立?若存在,求出适合条件的所有实数m;若不存在,说明理由.
答案:
解析:
解析:
首先证明①f (0)=0.②f (x)在R上递增.假设存在m. 原命题 又
|

练习册系列答案
相关题目
 t∈[0,1].
t∈[0,1].
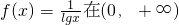 是减函数;
是减函数;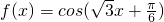 ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数;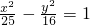 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5; 是减函数;
是减函数; ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数; 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5;