题目内容
在平面直角坐标系xOy中, 已知点A(0,-1),B点在直线![]() 上,M点满足
上,M点满足![]() ,
,![]() ,M点的轨迹为曲线C.
,M点的轨迹为曲线C.
(I)求C的方程;
(II)P为C上动点,![]() 为C在点P处的切线,求O点到
为C在点P处的切线,求O点到![]() 距离的最小值.
距离的最小值.
解:
(Ⅰ)设M(x,y),由已知得B(x,-3),A(0,-1).
所以![]() =(-x,-1-y),
=(-x,-1-y), ![]() =(0,-3-y),
=(0,-3-y), ![]() =(x,-2).
=(x,-2).
再由题意可知(![]() +
+![]() )•
)• ![]() =0, 即(-x,-4-2y)• (x,-2)=0.
=0, 即(-x,-4-2y)• (x,-2)=0.
所以曲线C的方程式为y=![]() x
x![]() -2.
-2.
(Ⅱ)设P(x![]() ,y
,y![]() )为曲线C:y=
)为曲线C:y=![]() x
x![]() -2上一点,因为y
-2上一点,因为y![]() =
=![]() x,所以
x,所以![]() 的斜率为
的斜率为![]() x
x![]()
因此直线![]() 的方程为
的方程为![]() ,即
,即![]() 。
。
则O点到![]() 的距离
的距离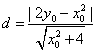 .又
.又![]() ,所以
,所以
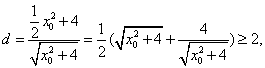
当![]() =0时取等号,所以O点到
=0时取等号,所以O点到![]() 距离的最小值为2.
距离的最小值为2.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是