题目内容
cos300°= ( )
A.- | B.-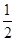 | C.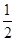 | D. |
C
解析试题分析:利用诱导公式把要求的式子化为 cos(360°-60°)=cos60°,由此求得结果.解:cos300°=cos(360°-60°)=cos60°=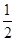 ,故选C
,故选C
考点:诱导公式和特殊角的三角函数值
点评:本题主要考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
如果 ,那么角
,那么角 的终边所在的象限是
的终边所在的象限是
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
 的值( )
的值( )
A.小于 | B.大于 | C.等于 | D.不存在 |
 的值域是( )
的值域是( )
A. | B. | C. | D. |
若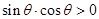 ,则
,则 在( )
在( )
| A.第一、二象限 | B.第一、三象限 |
| C.第一、四象限 | D.第二、四象限 |
定义在 上的偶函数
上的偶函数 满足
满足 若
若 时解析为
时解析为 ,则
,则 >0的解集是
>0的解集是
A. | B. |
C. | D. |
若点P(sinα-cosα,tanα)在第一象限,则在[0,2p)内α的取值范围是 ( )
A.( , ,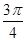 )∪(p, )∪(p,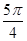 ) ) | B.( , , )∪(p, )∪(p,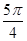 ) ) |
C.( , ,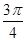 )∪( )∪(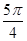 , ,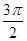 ) ) | D.( , ,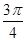 )∪( )∪(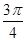 ,p) ,p) |
如图所示,是函数y=Asin(ωx+φ)(A>0,ω>0, -p<φ<0)的简图,则振幅、周期、初相分别是 ( )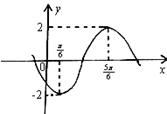
A.2, ,? ,? | B.2, ,? ,?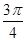 |
C.4, ,? ,?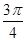 | D.2,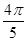 ,? ,? |
函数 ,
, 的值域是
的值域是
A. | B. | C. | D. |