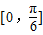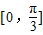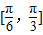题目内容
记O为坐标原点,已知向量
=(3,2),
=(0,-2),又有点C,满足|
|=
,则∠ABC的取值范围为( )
| OA |
| OB |
| AC |
| 5 |
| 2 |
分析:根据
的模为定值,利用圆的定义判断出C的轨迹为圆,结合图形,判断出BC与圆相切时或当A,B,C三点共线时,求得∠ABC的取值范围.
| AC |
解答: 解:∵|
解:∵|
|=
,点C在以点A为圆心,
为半径的圆周上.
可得|
|=5,如图可知,
当直线BC与圆周相切时,∠ABC有最大值为
,
当A,B,C三点共线时∠ABC有最小值为0,
所以∠ABC的取值范围为[0,
].
故选A.
 解:∵|
解:∵|| AC |
| 5 |
| 2 |
| 5 |
| 2 |
可得|
| AB |
当直线BC与圆周相切时,∠ABC有最大值为
| π |
| 6 |
当A,B,C三点共线时∠ABC有最小值为0,
所以∠ABC的取值范围为[0,
| π |
| 6 |
故选A.
点评:本题考查向量在几何中的应用、求角最值的方法:数形结合的思想方法.当动点的轨迹能判断出时,常采用此法.

练习册系列答案
相关题目
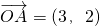 ,
, ,又有点C,满足
,又有点C,满足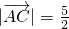 ,则∠ABC的取值范围为
,则∠ABC的取值范围为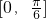
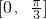

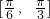
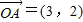 ,
,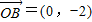 ,又有点C,满足
,又有点C,满足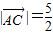 ,则∠ABC的取值范围为( )
,则∠ABC的取值范围为( )