题目内容
如图,正四棱柱ABCD—A1B1C1D1,AA1=
(1)求证:EM∥A1B1C1D1;
(2)求二面角B-A1N-B1的正切值.
解法一:(1)证明:取A1B1的中点F,连结EF,C1F.

∵E为A1B中点,
∴EF![]()
![]() BB1.
BB1.
又∵M为CC1中点,∴EF![]() C1M.
C1M.
∴四边形EFC1M为平行四边形.
∴EM∥FC1.
而EM![]() 平面A1B1C1D1,FC1
平面A1B1C1D1,FC1![]() 平面A1B1C1D1,
平面A1B1C1D1,
∴EM∥平面A1B1C1D1.
(2)由(1)EM∥平面A1B1C1D1,EM![]() 平面A1BMN,
平面A1BMN,
平面A1BMN∩平面A1B1C1D1=A1N,
∴A1N∥EM∥FC1.
∴N为C1D1中点,过B1作B1H⊥A1N于H,连结BH,根据三垂线定理BH⊥A1N,
∴∠BHB1即为二面角B-A1N-B1的平面角.
设AA1=a,则AB=2a,
∵A1B1C1D1为正方形,

∴A1N=![]() a,
a,
又∵△A1B1H∽△NA1D1,∴B1H=![]() .
.
在Rt△BB1H中,tan∠BHB1= ,
,
即二面角BA1NB1的正切值为![]() . 1
. 1
解法二:(1)证明:建立如图所示空间直角坐标系,设AB=2a,AA1=a(a>0),则
A1(2a,0,a),B(2a,2a,0),C(0,2a,0),C1(0,2a,a).
∵E为A1B的中点,M为CC1的中点,
∴E(2a,a,![]() ),M(0,2a,
),M(0,2a,![]() ),
),
∴EM∥平面A1B1C1D1.
(2)设平面A1BM的法向量为n=(x,y,z),又![]() =(0,2a,-a),
=(0,2a,-a),![]() =(-2a,0,
=(-2a,0,![]() ),
),

由n⊥![]() ,n⊥
,n⊥![]() ,
,
得 ,
,
∴ ∴取n=(
∴取n=(![]() ,
,![]() ,a).
,a).
而平面A1B1C1D1的法向量n1=(0,0,1),设二面角为θ,
则|cosθ|=![]() ,
,
又二面角为锐二面角,∴cosθ=![]() ,
,
从而tanθ=![]() .
.

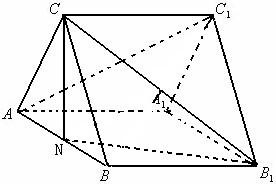 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
